Introduction

Differential hydro-mechanical variator is designed for automatic continuous variable transformation of rotational motion between the motor shaft and the shaft of the working body of the machinery for ensuring the optimal mode of joint work of the engine and the variator at arbitrarily changing value of the external load on the working body.

Differential hydro-mechanical variators can be very diverse in their kinematic scheme and structure. Differential hydro-mechanical variator can be regarded as consisting of two hydro-mechanical differential mechanisms differing from the already known ones by the hydraulic connection between kinematic units representing a differential schemes of gear hydraulic machines enabling to get different values of hydraulic and mechanical power flow distribution and provides automatic control of the differential hydro-mechanical variator parameters. At the same time mechanical differential mechanism with a different number of internal gear and an additional number of gears may be added to the kinematic scheme of the variator to increase the transformation rate.

Designing of differential hydro-mechanical variator is a hard complex problem, its solution can be divided into three distinct steps. The first step of the design is to establish the kinematic scheme of the variator. The second stage of the design is to develop constructive forms of the mechanism. The third step of a design process is to develop technological and economic indicators of the designed mechanism [1].

Power analysis of hydro-mechanical differential mechanisms

Unlike the conventional differential mechanism, relationship between the torques in the hydro-mechanical differential gear is determined by the equation [2, 3]

where  –M_TH-  the torque of the hydraulic pump attached to the master link, N·m;  – M _{H –} external load applied to the cage of differential, N·m; ,  –M_1, M₂

hydrostatic resistance moments acting respectively on the master and slave wheels of the hydraulic pump, N·m.

The relationship between the hydrostatic moments of resistance on the driving and driven tooth gears is determined by the ratio λ_H [2]:

According to the virtual displacement principle we can write

where N_H – the mechanical power flow in hydro-mechanical differential mechanism; N_Г – power hydraulic flow in hydro-mechanical differential mechanism.

Power of the hydraulic flow is divided into two streams, one of which is implemented on the driving wheel, and the second – on a driven wheel

where ,  –ω₁,  ω₂ the relative angular velocity of rotation of driving and driven wheels of the hydraulic pump.

Equation (4) with (2) can be written

The relative angular velocity of the driving wheel in the hydraulic pump can be represented by the following equation

Then the power of the hydraulic flow

Equation (3) represents balance of the powers in hydro-mechanical differential mechanism, which takes the following form

The moment on the carrier is determined by the resistance moment at the driven wheel by the formula

Considering the equation (6) the balance of power can be written

For graphing the moments and the power balance from the equation (7) it is necessary to deduce the dependence .

Equation (10) shows that the moment value of the resistance hydrostatic forces on the driven wheel is influenced by the parameters of hydro-mechanical differential mechanism, namely the transmission ratio of the hydraulic pump and the coefficient λ_H.

Designing of the kinematic scheme.

Kinematic differential circuit of the hydro-mechanical variator designing involves determination of the optimal schemes of hydro-mechanical differential mechanisms being kinematic units of the variator and their gear ratios selection basing on the equilibrium condition of the variator (carrier) rotor at a maximum coefficient of transformation. It is necessary to take into consideration some additional conditions related to structural requirements.

Kinematic scheme of the differential hydro-mechanical variator composed of two hydro-mechanical differential mechanisms with tooth gears of external engagement is shown in Figure 1. This scheme has a high efficiency value at the fluid pressure of 10-15 MPa and is applicable in transmissions of passenger cars with a maximum transformation ratio of less than 5. At determining the gear ratios of the kinematic units in the variator scheme shown in Figure 1, we have to give the proper maximum transformation ratio and the gear ratio of the differential hydro-pump [4, 5].

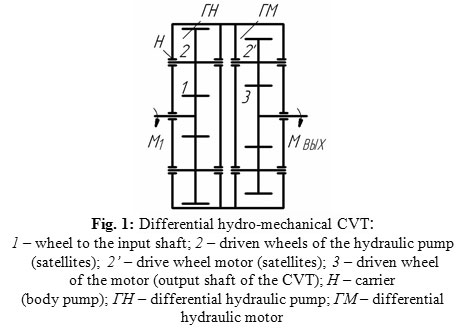Figure 1: Differential hydro-mechanical CVT: 1 – wheel to the input shaft; 2 – driven wheels of the hydraulic pump  (satellites); 2’ – drive wheel motor (satellites); 3 – driven wheel of the motor (output shaft of the CVT); Н – carrier (body pump); ГН – differential hydraulic pump; ГМ – differential hydraulic motor click here to view figure

1 – wheel to the input shaft; 2 – driven wheels of the hydraulic pump (satellites); 2’ – drive wheel motor (satellites); 3 – driven wheel of the motor (output shaft of the CVT); Н – carrier (body pump); ГН – differential hydraulic pump; ГМ – differential hydraulic motor

When the carrier of the variator is fixed, the torque from an external power source is transmitted to the input unit of the differential pump. At the transfer of the maximum torque, the reaction torque from the differential pump is acting on the carrier, and is defined by the formula:

where М₁ – summing up the moment, N∙m; i₂₁ – the gear ratio of the differential hydraulic pump; λ_н – the hydrostatic coefficient of redistribution of moments in the hydraulic pump; η_Н1 – The efficiency of the mechanical power flow in differential pump.

This moment has a direction coinciding with the direction of the variator input unit rotation. The relative rotation of the differential pump tooth gears creates a flow of hydraulic operating fluid, which causes the torque on the output shaft of the differential motor [6].

where i_г – hydraulic gear ratio of the variator; η_ГН – efficient hydraulic power flow in differential pump; η_ГМ – efficient hydraulic power flow to the differential hydraulic motor; К_max – the maximum ratio of the variator.

Hydraulic gear ratio required for provision of the maximum transformation ratio is defined by the formula:

where V_ОМ – the working volume differential motor, m³; V_ОН – the working volume differential hydraulic pump, m³.

The carrier also takes a reactive torque from the differential hydro-motor directed opposite the rotation of the variator input unit and deduced as

where λ_м – the coefficient of redistribution of moments in a hydrostatic motor; i_2’3 – the gear ratio of the differential hydraulic motor; η_Н2 – the efficiency of the mechanical power flow in the differential hydraulic motor.

Equilibrium condition of the differential hydro-mechanical variator carrier

Thus, the gear ratio of the differential motor is determined from the equation (16) at the given gear ratio of the differential hydraulic pump and a maximum transformation ratio of the variator.

After determining the kinematic parameters of the differential hydro-mechanical variator units, it is necessary to define structural and geometrical parameters including displacements, and the multiplicity of differential hydraulic pump and motor action, their module, the number of teeth and the width of the gear.

To reduce the size of hydraulic machines, all other things being equal, it is desirable to choose a possibly least number of teeth, and a largest module [7, 8]. Positive bias of the initial circuit is performed to eliminate the cropping of teeth legs.

Displacement of the differential pump is determined by the maximum torque of the engine and the pressure of the working fluid

where М_emax – the maximum torque of the engine, N∙m; p_н – the pressure of the working fluid, МPa; k_н – the multiplicity of the action of the pump.

Displacement of the differential motor is determined by the formula:

where k_м – the multiplicity of the action of the motor.

At the given displacement of the hydraulic machine, the number of gear teeth and their width ratio, we can predetermine the module value from the equation

where V₀ – the working volume of the hydraulic machine, mm³; z – the number of gear teeth, which defines the working volume of the hydraulic machine; x – the offset of the original contour; ψ_bm – the ratio of the width of the gear.

The gear width is calculated after determining the engagement module

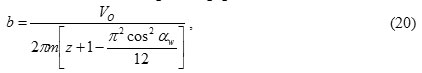
where α_w – the angle gear.

The above procedure was applied for designing the continuous variable automatic transmission for the small light vehicle and determining its basic parameters (Figure 2).

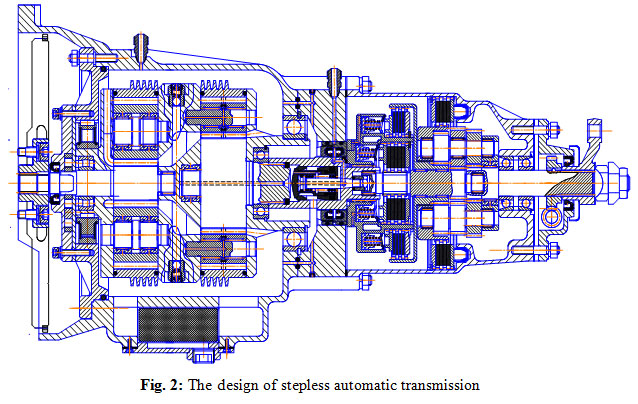Figure 2: The design of stepless automatic transmission clock here to view figure

Conclusion

The method proposed for continuous variable transmission designing on the basis of differential hydro-mechanical variators consisting in a consecutive choice of gear ratios of the  kinematic units in the mechanism from the conditions of the rotor variator (carrier) equilibrium, as well as the main parameters of tooth gear engagements providing the necessary displacement of the  hydraulic machines for maximum torque transmission, enables to choose the main kinematic and power transmission parameters for different classes of vehicles, to evaluate the effect of these parameters on the car haulage and speed capacities at the designing stage and implement optimization of the selected parameters on the basis of operating conditions. A designed continuous variable gearbox of a car enables to change automatically and continuously the traction on the wheels depending on the vehicle speed.

References

1. Sharipov V.M. Building and calculation of tractors / Moscow: Publishing Mechanical Engineering, (2004). – 590 p.
2. Mavleev, I.R. Development of efficient schemes and designs high-torque hydromechanical CVTs for vehicles: Author. dis. Cand. tehn. Sciences. – Naberezhnye Chelny, (2007). – 19 p. [Мавлеев И.Р. Разработка рациональных схем и конструкций высокомоментных гидромеханических вариаторов для транспортных средств: Автореф. дис. Канд. техн. Наук. – Набережные Челны, (2007). – 19 с.]
3. Salakhov, I.I. The development of automatic transmissions rational schemes, based on the planetary system of universal multi-threaded differential mechanism: Author. dis. Cand. tehn. Sciences. – Izhevsk: M.T.Kalashnikov IzhSTU, (2013). – 23 p. [Салахов И.И. Разработка рациональных схем автоматических коробок передач на основе планетарной системы универсального многопоточного дифференциального механизма: Автореф. дис. Канд. техн. Наук. – Ижевск: ИжГТУ М. Т. Калашников (2013). – 23 с.]
4. Patent №2347966 RF IPC F16H 47/04. Differential hydro-mechanical high-torque CVT / Voloshko V.V., & Mavleev I.R. Publ. 27.02.2009, Bull. № 6. [Патент №2347966 РФ, МПК F16H 47/04. Высокомоментный дифференциальный гидромеханический вариатор / Волошко В.В., & Мавлеев И.Р. Опубл. 27.02.2009, бюл. №6.]
5. Patent №2384773 RF IPC F16H 3/44. Automatic speed planetary gearbox / Voloshko V.V., & Salahov I.I. Publ. 20.03.2010, Bull. № 8. [Патент №2384773 РФ, МПК F16H 3/44. Автоматическая ступенчатая планетарная коробка передач/ Волошко В.В., & Салахов И.И. Опубл. 20.03.2010, бюл. №8.]
6. Ildar Ilgizarovich Salakhov*, Vladimir Vladimirovich Voloshko, Ilnur Dinaesovich Galimyanov and Ildus Rifovich Mavleev Universal Differential Mechanism / Biosciences Biotechnology Research Asia, Vol. 11(3), 2014, 1553-1557 pp., https://www.biotech-asia.org/currentissue.php?pg=2
7. Ildar Ilgizarovich Salakhov*, Ildus Rifovich Mavleev, Ildar Rafisovich Shamsutdinov, Ruslan Ramilevich Basyrov and Voloshko Vladimir Vladimirovich Research and Development of Hydro-Mechanical Differential Variator / Biosciences Biotechnology Research Asia, September 2015., Vol. 12(1), 619-625 pp., http://dx.doi.org/10.13005/bbra/1705
8. Ildar Ilgizarovich Salakhov*, Ildus Rifovich Mavleev, Eduard Nikolaevich Tsybunov, Ruslan Ramilevich Basyrov and Niyaz Ilgizarovich Salakhov Car Gearbox on the Basis of the Differential Mechanism / Biosciences Biotechnology Research Asia, September 2015., Vol. 12(Spl. Edn. 2), 41-44 pp., https://www.biotech-asia.org/specialedition.php?issue=SE%20SEP%2015