How to Cite | Publication History | PlumX Article Matrix
Davoud Fani and Elmira Shahraki
Department of Electrical and Computer Engineering, University of Sistan and Baluchestan, Zahedan, Iran
DOI : http://dx.doi.org/10.13005/bbra/2075
ABSTRACT: Fractional order (FO) controllers are highly considered with regard to higher performance and robustness of these controllers in FO systems. According to advantages of PID controllers such as suitable performance, low price and simplicity of design, they are widely used in industry. A FOPID controller is used for two-link robot control in this paper. Considering vast use of evolutionary algorithms and numerical optimization, coefficients of the FO controller are optimized using evolutionary algorithms in this paper. An individual FOPID controller is applied in order to control each link. Three evolutionary optimization algorithms including particle swarm optimization (PSO), genetic algorithm and estimation of distribution algorithm, are compared from optimal coefficients determination point of view. Experimental results indicate that FOPID controller is more applicable according to use of actual model for robot and suitable performance of the PSO algorithm.
KEYWORDS: evolutionary algorithms; fractional order controller; PID controller; two-link robot
Download this article as:| Copy the following to cite this article: Fani D, Shahraki E. Two-link robot manipulator using fractional order PID controllers optimized by evolutionary algorithms. Biosci Biotech Res Asia 2016;13(1) |
| Copy the following to cite this URL: Fani D, Shahraki E. Two-link robot manipulator using fractional order PID controllers optimized by evolutionary algorithms. Biosci Biotech Res Asia 2016;13(1). Available from: https://www.biotech-asia.org/?p=7706 |
Introduction
Along with introduction of fractional order (FO) controllers and their higher performance and robustness on FO systems by Podlubny in 1994, FO systems and their control process are significantly considered [1]. Although PID controllers are introduced long time ago, they are widely used in industry because of their advantages such as low price, design simplicity and suitable performance [2, 3]. While three parameters of design including proportional (), integral (), and derivative () are available in PID controllers, two more parameters exist in FOPID controllers for adjustment. These parameters are integral fractional order and derivative fractional order [4]. In comparison with PID controllers, FOPID controllers have more flexible design that result in more precise adjustment of closed-loop system [5]. FOPID controllers are defined by FO differential equations. It is possible to tune frequency response of the control system by expanding integral and derivative terms of the PID controller to fractional order case. This characteristic result in a more robust design of control system, but it is not easily possible [6].
According to non-linearity, uncertainty, and confusion behaviors of robot arms, they are highly recommended for experimenting designs of control systems. Despite non-linear behavior of robot arm, it is demonstrable that a linear proportional derivative controller can stabilize the system using Lyapanov [7]. But, classic PD controller itself cannot control robot to reach suitable condition. Several papers and wide researches in optimizing performance of the robot manipulator show the importance of this issue. Different adaptive and robust procedures are proposed for robot control that all of them are so complicated in analysis and design [8-11]. Approaches that have been proposed for robot control are categorized in non-linear methods that are more difficult than linear methods in analysis and implementation [12-14].
In this paper, individual FOPID controllers are applied for controlling two-link robot arm with non-linear treatment. On the other hand, evolutionary optimization algorithms such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Estimation of Distribution Algorithm (EDA) are used to determine optimal parameters for the controllers in such non-linear systems.
In the following, literature review is provided at first and then fractional order concepts and FOPID are described. Introductions of evolutionary optimization algorithms, model of the robot, proposed method, and experimental results are provided, respectively. Finally, paper is discussed and concluded.
Related Work
A partial differential equation dynamic model is proposed in [15] to regulate joint position and suppress elastic vibration of a flexible two-link controller with different payloads. Approximate stability of closed-loop system and effectiveness of the proposed method are validated theoretically and numerically. A new non-linear partial differential equation observer is proposed in [16] to control a flexible two-link robot. A singular perturbation approach is also used for analyzing rigidity-flexibility coupling dynamics.
In order to control active magnetic bearing system, a FOPID controller is proposed in [17] using an adaptive GA for multi-objective optimization. It is proved that FOPID has impressive effect on overshoot and settling time reduction. Another optimal FOPID controller was proposed in [18] for a full vehicle non-linear active suspension system. An electromagnetism-like algorithm and GA based FOPID design is proposed in [19] for second order system with time delay. Proposed algorithm has faster convergence and better global optimization capability.
In another approach a hybrid LQ-fuzzy controller is proposed for the purpose of two-link robot control [20]. Not only does the proposed method provide robustness but also it does not increase the order of the whole complex non-linear system. In [21] uncertain parameters are modeled as fuzzy variables and using fuzzy dynamic analysis, a two-link robot controller is studied.
Differential evolution (DE) algorithm is also used in [22] for PID controller adjustment in unstable and integrating processes with time delay. A differential evolution algorithm based FOPID controller is used in [23]. PSO, GA, and DE algorithms were compared in second order and FO plants and also in speed control of a DC motor. Experimental results show that better solutions were found by DE-based methods consuming less computational time.
In order to overcome defects of traditional two-link robot controllers such as non-linear characteristics and uncertainties, a combination of
neural network and linear controller is used in [24]. In this approach, non-linear model is converted to linear model and unknown parameters of the system are recognized by neural network with special learning rules. Finally, a stabilized closed-loop system is obtained using linear feedback-H∞ control method. An H∞ loop-shaping design feedback controller and a command pre-shaping filter as feed-forward controller are used in [25] as two-link robot controller. It can control joint angles of the robot arm and suppress vibrations of the system, simultaneously using proper loop shape.
In [26] parameters of a FO controller were optimized using modified PSO that has better solution and faster search speed in contrast with GA. By using PSO in [27], a FOPID controller was designed that has remarkable reduction in overshoot, rise time and setting time. In another approach, the PSO was applied to determine FOPID parameters with efficient search and more robust performance using for an automatic voltage regulator [28]. A novel Adaptive PSO was also used in [29] to find optimal parameters of PID controller and unstable non-linear system.
A two-degrees-of-freedom planar robot, which is not actual and practical, was controlled by FOPID controller optimized with PSO and GA evolutionary algorithms in [30]. Performances of the evolutionary algorithms are compared using different cost functions. Simulation results show that the FOPID controller has better performance while using PSO algorithm for tuning instead of using GA.
Fractional Order Concepts And Fopid Controller
Fractional Order Calculations
In order to study about FO controllers, mathematical concepts and FO systems should be analyzed at first. FO calculation is a branch of correct order calculations that tries to find possibility of fractional order integral and derivative being. Among all definitions for FO integral and derivative, Riemann-Liouville, Grunwald-Ltnykuf, and Caputo that include Cauchy integral, are more useful than others. Thus, the general form of derivative-integral fractional operator will be defined as follows:

where the correct order of derivative-integral operator is defined with q and parameter that represents the fractional integral or derivative is defined with t. a denotes lower limit of derivative and integral. Among above mentioned definitions of fractional order, Grunwald-Ltnykuf is the most common and widely used definition which is defined as follows [31]:

General arithmetic operator that includes order of derivative and integral is also expressed as follows:
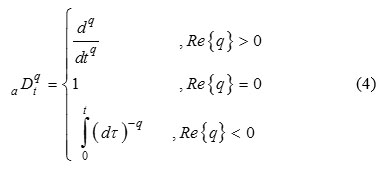
A FO system in time domain can be defined by a FO differential equation as below:
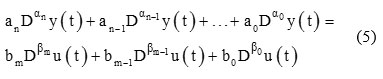
General form of the FO transform function can be achieved by applying the Laplace transform on equation as below:
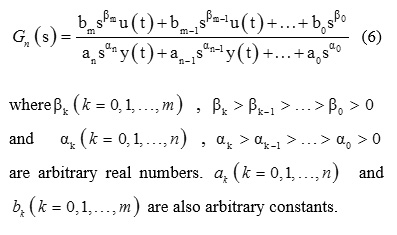
where and are arbitrary real numbers. and are also arbitrary constants.
Fopid Controller
FOPID controllers are General form of correct order PID controllers that classic integral and derivative terms are replaced by order integral and order derivative terms. Differential equation of FOPID controller can be defined as follows:
![]()
By applying the Laplace transform to equation (7) we have:
Regarding equation (8), it is obvious that the conventional PID controller can be achieved by setting λ = 1 and μ = 1 . So, it can be said that the correct order PID controller is a special case of FOPID controller in which the order of derivative and integral terms are set to 1. As shown in the definition of Riemann-Lionville [32], dimensions of the FO systems are infinite. So, because of two additional parameters in FO controllers, they are highly flexible in design and of course these designs are more complicated, consequently.
Evolutionary Optimization Algorithms
Particle Swarm Optimization (Pso)
PSO algorithm by Eberhart and Kennedy was presented as a model of local motion for group of animals. This algorithm is applied on various issues such as minimizing cost function, non-linear mapping, training neural networks, neural network inversion, and data mining as well. The algorithm includes a bunch of particles. Each of which can be shown to be optimal response to the problem of optimization. The algorithm continuously updates the position of each particle by calculating particle velocity and applying that to the position of the particle. If is position of ith particle at time t, position of the particle at each time is calculated as [33]:
![]()
Structure of the algorithm is in a manner that all particles are perfectly linked together. In each time cycle, all particles are updated by social component of the best particle which is resulted from all particles. This component is called. Velocity is calculated as follows:
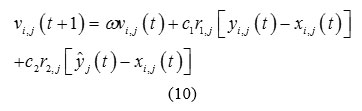
where vij(t) denotes velocity of ith particle in jth dimension at time t.,andare constants which are weight of inertia, coefficient of personal training, and coefficient of global training, respectively. They are used to adjust the cognitive and social components.
Pseudo-code of the PSO algorithm is:
- Determine and initialize the position and velocity of the particles.Obtain a cost function for each particle and d
- etermine the best particle (the smallest value of the cost function)
- Until the stop conditions have been established:
- Update velocity and position of particles regarding the position of the best particle.
- Obtain cost function of all particles and determine the best particle.
- Update the global optimal.
- End of the algorithm.
Genetic Algorithm (Ga)
GA can be called as a global search method that mimics the natural laws of biological evolution.
This algorithm obtains better approximation of final response in each generation using selection process which is proportional to the value of responses and reproduction of selected responses. It is done by using operators which are emulated from natural genetic. This process makes the new generations to be consistent with the conditions of the issue. Before the implementation of a GA, an appropriate presentation must be found for the intended issue. The most common way to form chromosomes in GAs is binary strings. Therefore, each decision variable is designed in a binary form and then chromosome is made by getting these variables together. Although this method is the most extensive coding scheme, but other methods such as display with real numbers are growing. A fitness function must also be devised to attribute proper value to each coding solution. During the process, the parents are selected for breeding and mating and mutation operators are combined together to produce new offspring. This process is repeated several times to produce next generation population. Then the population will be investigated and if the convergence measures are met, this process is terminated. Pseudo-code of the GA is as follows [34]:
- Determine and initialize chromosomes
- Obtain a cost function for each chromosome and determine the best chromosome (with the smallest cost function)
- Until the stop conditions have been established:
- Select the chromosomes of parents with regard to the accuracy of previous population
- Crossover: Do fertility and creating a new generation
- Mutation: Determine place of new offspring produced in chromosomes
- Acceptance: Accommodate new offspring in the population
- Replacement: Replace new population instead of previously used and apply for later stages of the algorithm
- End of the algorithm.
Estimation Of Distribution Algorithm (Eda)
EDA is a new concept in the field of evolutionary computation which is emerged with the idea of making a probabilistic and selective model of the population. These algorithms do not relay on large genetic basis, but a distinct possibility model for distribution of selected people in the search space is made for every generation. Like the classic GA, all types of EDAs will begin the process with an initial population. Then numbers of basic people are selected and parent generations are replaced by new offspring according to estimation of basic people distribution. In fact, mutation and crossover operations in GA are replaced by a unit whose job is to estimate the distribution and sampling new people. In this algorithm, the direct role of the parent in reproduction is attenuated. Parents are not producing children but overall distribution of parents result in producing children. Unlike genetic based algorithms which implicitly doing the processing on structural blocks, processing of EDA is explicitly depended on use of probabilistic model. Whatever the accuracy of this probabilistic model is higher, the algorithm effectively avoids destruction of important structural blocks [35]. Pseudo-code of the EDA is as follows:
- Determine and initialize the population
- Obtain the cost function for each person of population
- Until the stop conditions have been established:
- Select the top people of the whole population
- Calculate the distribution probability of selected people
- Reproduce according to the distribution probability
- Acquire new cost function for each person of the population
- Replace new population instead of the previously used and apply for later steps of the algorithm
- End of the algorithm.
Robot Model
The model of a robot arm with two degrees of freedom in vertical plane examined in the proposed method is shown in Fig.1. This robot with two degrees of freedom is part of an industrial robot with six degrees of freedom or two end joints of an artist arm. It can be said that control of the second and third joints in a robot with six degrees of freedom are the most complex ones. While they have to endure full weight of engines and gearboxes, so much torque is applied to the second and third joints. Standard model proposed for hard joint robot arm is usually as follows [36]:
![]()
where q ⊂ R2 denotes relations position vector, D(q) I R2X2 stands for moment of inertia matrix, and C(q,q)q ⊂ R2 is vector of Coriolis acceleration and from center acceleration. G(q) ⊂ R2 is gravitational acceleration vector, and τm ⊂ R2 denotes engines torque vector. Equations of non-linear robot are multivariable with multi-inputs and multi-outputs and external disturbance also adds complexity. This complexity is one of the major challenges in modeling and controlling the robot.
According to more real and practical feature of the robot model in this paper, expression is obtained as follows [35]:
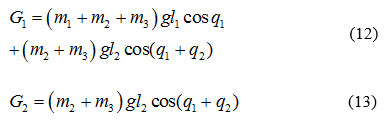
Material of body and weight of arms are changed with regard to above relations. Accordingly, robot model becomes closer to actual and practical model and non-linearity of the system is increased.
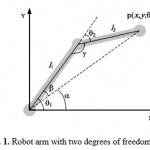 |
Figure 1: Robot arm with two degrees of freedom |
Proposed Method
While non-linear controllers are of high complexity and single-loop robot arm control using the classic controller is not possible, a linear double-loop controller for controlling robot arm is considered in this paper to achieve optimal performance. Real robot arm model [36] is used for practical condition that described in section 5 and a separate FOPID controller is used for each individual link of the robot arm. Indeed, both links of robot arm are controlled in parallel with the aim of tracking the input desired trajectory. Due to non-linearity of the system, a linear controller design with conventional methods is not helpful. In this regard, the evolutionary optimization algorithms including GA, PSO, and EDA are used to determine the optimal parameters of controller. The proposed algorithm shows that linear controller is capable of controlling a non-linear system with all complexities. Considering more practical robot model and increased non-linear performance, the proposed method is compared with [30] from controlling point of view. Also, the proposed scheme is evaluated for appropriate operation of optimization algorithms. According to the obtained results from feasibility and usability points of view, the proposed method is more suitable for implementation.
Simulation Results
In order to evaluate the proposed approach in MATLAB software environment, modeling the robot arm is done first. Then, robot model and control system are simulated in MATLAB Simulink as in
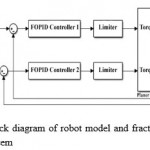 |
Figure 2: Block diagram of robot model and fractional order control system |
Fig. 2 to evaluate the performance of FOPID controller in controlling two-link robot.
At first, dynamic model of two-link robot [36] is implemented with following numerical values to evaluate performance of FOPID controller and to compare performance of optimization algorithms in finding optimal coefficients.
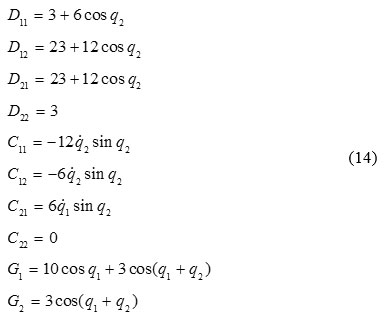
Also, desired trajectory for the robot will be as follows [30]:
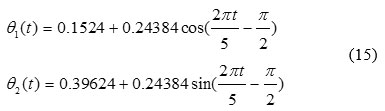
MRSE is the object function of optimization problem. Its relation is as follows:
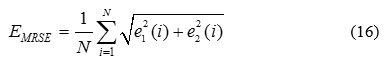
Table 1: Simulation parameters
| Max Iterations | 100 | |
| Number of population | 50 | |
| PSO | C1 = C2 | 1.429 |
| W | 0.729 | |
| GA | Crossover Ratio | 0.7 |
| Mutation Ratio | 0.2 | |
| EDA | Estimation Ratio | 0.7 |
In the study on optimization algorithms, utilized simulation parameters are in accordance with table 1.
After simulations, the optimal coefficients of FOPID controller using PSO, GA, and EDA are obtained as in table 2. As mentioned above, evaluation criterion is MRSE that is a type of error criteria. Despite the real robot model and increased non-linear behavior, optimal coefficients are smaller and the proposed controller gives better control operations, so it is more practical and suitable for implementation. Graphical results of tracking the first desired trajectory by controlled robot using FOPID controller optimized with GA, EDA, and PSO optimization algorithms are shown in Fig. 3, Fig. 4, and Fig. 5, respectively.
Table 2: Tuned parameters of the designed FOPIλDμ controller with the PSO, GA, and EDA for the MRSE
| FOPID
Params |
PSO | GA | EDA | |||
| Link1 | Link2 | Link1 | Link2 | Link1 | Link2 | |
| Kp | 529.950 | 142.671 | 770.981 | 373.486 | 780.955 | 151.533 |
| Kt | 579.127 | 240.389 | 295.968 | 249.242 | 593.864 | 284.332 |
| Kd | 324.012 | 337.252 | 159.586 | 327.220 | 280.962 | 132.758 |
| λ | 0.158 | 0.385 | 0.749 | 0.293 | 0.374 | 0.189 |
| 0.431 | 0.611 | 0.842 | 0.473 | 0.415 | 0.284 | |
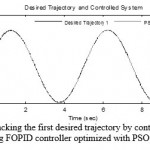 |
Figure 3: Tracking the first desired trajectory by controlled robot using FOPID controller optimized with PSO |
 |
Figure 4:Tracking the first desired trajectory by controlled robot using FOPID controller optimized with GA |
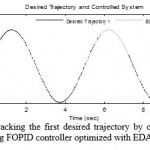 |
Figure 5: Tracking the first desired trajectory by controlled robot using FOPID controller optimized with EDA |
As can be observed in Fig.3, PSO algorithm is able to track the first desired trajectory after almost 0.8 s. It is also observed that PSO has good performance in positive and negative peaks of desired trajectory and the path is followed with minimum error. According to Fig. 4, it can be seen that GA is able to track the first desired trajectory after about 0.7 s. the algorithm has relatively good performance in positive and negative peaks of desired trajectory. The EDA could track the first desired trajectory after nearly 0.5 s. It can be observed in Fig. 5 that the algorithm has acceptable performance in positive peaks of desired trajectory while it has some errors in negative peaks.
Graphical results of tracking the second desired trajectory are also depicted in Fig. 6, Fig. 7, and Fig. 8, respectively.
 |
Figure 6: Tracking the second desired trajectory by controlled robot using FOPID controller optimized with PSO |
 |
Figure 7: Tracking the second desired trajectory by controlled robot using FOPID controller optimized with GA |
 |
Figure 8: Tracking the second desired trajectory by controlled robot using FOPID controller optimized with EDA |
It is observed in Fig. 6 that PSO algorithm could track the second desired trajectory after about 1.3 s with minimum error in positive and negative peaks. Regarding Fig. 7, GA is converged to the second desired trajectory after almost 1.1 s. It has acceptable performance in positive peaks but some errors are occurred in negative peaks during tracking. The EDA is depicted in Fig. 8 for the second desired trajectory that is converged after about 1.45 s with good performance in positive peaks. It has further errors than two other algorithms during tracking negative peaks. For more detailed comparison of performance in tracking, three optimization algorithms are shown in one figure for each desired trajectory as follows.
 |
Figure 9: Comparison the performance of PSO, GA, and EDA algorithms in design of optimized FOPID controller for the first desired trajectory |
 |
Figure 10: Comparison the performance of PSO, GA, and EDA algorithms in design of optimized FOPID controller for the second desired trajectory |
Table 3: Comparison tracking error of PSO, GA, and EDA algorithms
| Designed Controller | MRSE |
| PSO-FOPID | 0.001198 |
| GA-FOPID | 0.001461 |
| EDA-FOPID | 0.001642 |
According to the results shown in Fig. 9 and Fig. 10, FOPID controller optimized with evolutionary optimization algorithms have been able to control two links of a robot arm, simultaneously. Thus, desired trajectories are followed as well as possible.
To evaluate and compare the performance of optimization algorithms, the tracking error is shown in table 3 with MRSE measure. It can inferred from the results of table 3 that FOPID controllers optimized with PSO algorithm trace the desired trajectories with less tracking error than GA and EDA algorithms.
Conclusion
The application and operation of FOPID controllers to control the actual and practical two-link robot is studied in this paper. According to the non-linearity of the robot system, the design of such controllers for non-linear systems without use of optimization algorithms and using only trial and error, experimental, and conventional methods is very difficult or nearly impossible. So, in the controller design process, controller parameters are calculated using PSO, GA, and EDA algorithms. Regarding the simulation results, it is concluded that PSO algorithm shows better performance among three mentioned optimization algorithms. Also, the results indicate more suitability of implementation with regard to the actual robot model used in this paper. Therefore, it seems possible to design such controllers for robots with more degrees of freedom to reach desired performance.
References
- Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, United States, Academic press, 1998.
- K. Lee and J. M. Watkins, “Determination of all stabilizing fractional-order PID controllers,” in American Control Conference (ACC), IEEE, pp. 5007-5012, San Francisco, CA, 2011.
- Tehrani, A. Amirahmadi, S. Rafiei, G. Griva, L. Barrandon, M. Hamzaoui, et al., “Design of fractional order PID controller for boost converter based on multi-objective optimization,” in Power Electronics and Motion Control Conference (EPE/PEMC), 14th International, pp. 179 -185, Ohrid , 2010.
- Rai, V. Shekher, and O. Prakash, “Determination of stabilizing parameter of fractional order PID controller using genetic algorithm,” International Journal of Computational Engineering and Management, vol. 15, no. 1, pp. 24-32, 2012.
- Padula, and A. Visioli, “Tuning rules for optimal PID and fractional-order PID controllers,” Journal of process control, vol. 21, no. 1, pp. 69-81, 2011.
- Yeroglu, and N. Tan, “Note on fractional-order proportional-integral-differential controller design,” Control Theory & Applications, IET, vol. 5, no. 17, pp. 1978-1989, 2011.
- W. Spong, S. Hutchinson, and M. Vidyasagar, “Robot modeling and control, John Wiley & Sons, 2006.
- Fernandez, L. Penalver, V. Hernandez, and J. Tornero, “High performance algorithm to obtain Johansson adaptive control in robot manipulators,” Communications in Nonlinear Science and Numerical Simulation, vol. 9, no. 2, pp. 167-176, 2004.
- T. Abdallah, D. Dawson, P. Dorato, and M. Jamshidi, “Survey of robust control for rigid robots,” IEEE Control Systems, vol.11, no.2, PP. 24-30, 1991.
- Qu and D. M. Dawson, Robust tracking control of robot manipulators, USA, IEEE press, 1995.
- W. Spong, “On the robust control of robot manipulators,” Automatic Control, IEEE Transactions on, vol. 37, no. 11, pp. 1782-1786, 1992.
- H. Kim, C. Park, and F. Harashima, “A self-organized fuzzy controller for wheeled mobile robot using an evolutionary algorithm,” Industrial Electronics, IEEE Transactions on, vol. 48, no. 2, pp. 467-474, 2001.
- -H. Kim, C.-K. Park, and F. Harashima, “Adaptive fuzzy controller design for trajectory tracking of a 2 DOF wheeled mobile robot using genetic algorithm,” in Intelligent Robots and Systems, Proceedings, IEEE/RSJ International Conference on, pp. 1584-1589, Victoria, BC, 1998.
- M. Fateh, and S. Khorashadizadeh, “Optimal robust voltage control of electrically driven robot manipulators,” Nonlinear Dynamics, vol. 70, no. 2, pp. 1445-1458, 2012.
- Zhang, and J. Liu, “Adaptive boundary control for flexible two-link manipulator based on partial differential equation dynamic model,” Control Theory & Applications, IET, vol. 7, no. 1, pp. 43-51, 2013.
- Zhang, and J. Liu, “Observer-based partial differential equation boundary control for a flexible two-link manipulator in task space,” Control Theory & Applications, IET, vol. 6, no. 13, pp. 2120-2133, 2012.
- -Y. Chang, and H.-C. Chen, “Tuning of fractional PID controllers using adaptive genetic algorithm for active magnetic bearing system,” WSEAS Trans. Syst, vol. 8, no. 1, pp. 158-167, 2009.
- A. Aldair, and W. J. Wang, “Design of fractional order controller based on evolutionary algorithm for a full vehicle nonlinear active suspension systems,” International Journal of Control and Automation, vol. 3, no. 4, pp. 33-46, 2010.
- -H. Lee, and F.-K. Chang, “Fractional-order PID controller optimization via improved electromagnetism-like algorithm,” Expert Systems with Applications, vol. 37, no. 12, pp. 8871-8878, 2010.
- A. Hussain and M. B. Kadri, “Control of under-actuated two-link ROBOT with hybrid LQ-fuzzy controller,” in Robotics and Emerging Allied Technologies in engineering (iCREATE), International Conference on, Islamabad, pp. 174-179, 2014.
- Lara-Molina, E. Koroishi, and V. Steffen, “Uncertainty analysis of a two-link robot manipulator under fuzzy parameters,” in Robotics: SBR-LARS Robotics Symposium and Robocontrol (SBR LARS Robocontrol), Joint Conference on, Sao Carlos , pp. 1-6, 2014.
- Bingul, “A new PID tuning technique using differential evolution for unstable and integrating processes with time delay,” in Neural Information Processing, Springer Berlin Heidelberg, pp. 254-260, 2004.
- Biswas, S. Das, A. Abraham, and S. Dasgupta,’’ Design of fractional-order PIλDμ controllers with an improved differential evolution’’, Engineering Applications of Artificial Intelligence, vol.22, no.2, pp. 343–350, 2009.
- Moradi, and H. Malekizade, “Neural network identification based multivariable feedback linearization robust control for a two-link manipulator,” Journal of Intelligent & Robotic Systems, vol. 72, no. 2, pp. 167-178, 2013.
- sayahkarajy, Z. Mohamed, A. Faudzi, E. Supriyanto, and D. Owen, “Hybrid vibration and rest-to-rest control of a two-link flexible robotic arm using H∞ loop-shaping control design,” Engineering Computations, vol. 33, no. 2, 2016.
- -Y. Cao and B.-G. Cao, “Design of fractional order controllers based on particle swarm optimization,” in Industrial Electronics and Applications, 1ST IEEE Conference on, Singapore , pp. 1-6, 2006.
- Maiti, S. Biswas, and A. Konar, “Design of a fractional order PID controller using particle swarm optimization technique,” 2nd National Conference on Recent Trends in Information Systems (ReTIS-08), arXiv preprints arXiv: 0810.3776, 2008.
- Zamani, M. Karimi-Ghartemani, N. Sadati, and M. Parniani, “Design of a fractional order PID controller for an AVR using particle swarm optimization,” Control Engineering Practice, vol. 17, no. 12, pp. 1380-1387, 2009.
- Alfi, and H. Modares, “System identification and control using adaptive particle swarm optimization,” Applied Mathematical Modelling, vol. 35, no. 3, pp. 1210-1221, 2011.
- BİNGÜL, and O. KARAHAN, “Fractional PID controllers tuned by evolutionary algorithms for robot trajectory control,” Turkish Journal of Electrical Engineering & Computer Sciences, vol. 20, no. Sup. 1, pp. 1123-1136, 2012.
- Valério, and J. Sa da Costa, “Introduction to single-input, single-output fractional control,” Control Theory & Applications, IET, vol. 5, no. 8, pp. 1033-1057, 2011.
- Podlubny, “Fractional-order systems and fractional-order controllers,” Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, vol. 12, no. 3, PP. 1-18, 1994.
- Wei, and L. Qiqiang, “Survey on Particle Swarm Optimization Algorithm [J],” Engineering Science, vol. 5, no. 5, pp. 87-94, 2004.
- J. Grefenstette, “Optimization of control parameters for genetic algorithms,” Systems, Man and Cybernetics, IEEE Transactions on, vol. 16, no. 1, pp. 122-128, 1986.
- Wan, L. Mao, and G. Wang, “Estimation of distribution algorithm for a class of nonlinear bilevel programming problems,” Information Sciences, vol. 256, pp. 184-196, 2014.
- Sadati, and R. Ghadami, “Adaptive multi-model sliding mode control of robotic manipulators using soft computing,” Neurocomputing, vol. 71, no. 13, pp. 2702-2710, 2008.

This work is licensed under a Creative Commons Attribution 4.0 International License.





