How to Cite | Publication History | PlumX Article Matrix
Arash Ghenaat1 and Adel Johari Moghadam2 *
1AJA University of Medical Sciences, Tehran, Iran.
2Department of Cardiology, AJA University of Medical Sciences, Tehran, Iran.
Corresponding Author Email : adeljoharim@yahoo.com
DOI : http://dx.doi.org/10.13005/bbra/2099
ABSTRACT: Aterosclerosis and obstructions especially in great and vital arteries cause blood circulation system numerous disorders. Coronary arteries, carotid and femoral as the most important arteries could be affected negatively by aterosclerosis which may result in shock or heart attack. Bypass surgical operation is a significant method to treat clogged arteries nowadays and should be designed as perfect as it would minimize flow turbulence. Numeral simulation techniques are among the most recommended methods to reach this purpose. While most of researchers considered blood as a Newtonian fluid and none has studied magnetic field effect on bypass, we aimed to evaluate blood flow as a non-Newtonian fluid in presence of magnetic field and gravity acceleration in different bypass angels. A model of three-dimensional femoral artery with bypass and rigid wall was assumed. Percentages of blockage was defined by following formula; [(Ai – As)/Ai] in which Ai was non-blockage area, and As was the artery’s narrowest part area. Desired geometry was modeled by SolidWorks software then networked in Gambit software. There were three different equations applied including: Equation of the artery in the blockage area, sinusoidal relationship based on Reynolds number and fluid equation of continuity and momentum. Magnetic force of blood flow acted as a resistant tensional force and in presence of magnetic field normal blood flow was observed and subsequently outward viscosity was increased. Magnetic field also caused thickening boundary layer and as velocity gradient increased close to the walls shear stress enhanced. When magnetic field increased and Hartmann number enhanced subsequently there was no observation of negative shear stress. In the bypass entrance a returned flow occurred. By developing the Hartmann number vortex power decreased so that in 10 and 20 Hartmann returned flow was vanished completely. All of hemodynamic parameters and environmental factors that affect them are necessary to improve the efficiency of bypass surgical operations. If the three-dimensional modeling approaches maximally match with the reality they could help the specialists to choose the best location and angel of the bypass and improve the achievement probability significantly
KEYWORDS: Magnetic Field; Femoral Bypass Angles; Lipid Accumulations; Atherosclerosis Disease
Download this article as:| Copy the following to cite this article: Ghenaat A, Moghadam A. J. Evaluating the Effect of Magnetic Field, Impulse Flow and Gravity Acceleration on Different Femoral Bypass Angles in Order to Remove Lipid Accumulations in Atherosclerosis Disease by Simulation Method. Biosci Biotech Res Asia 2016;13(2). |
| Copy the following to cite this URL: Ghenaat A, Moghadam A. J. Evaluating the Effect of Magnetic Field, Impulse Flow and Gravity Acceleration on Different Femoral Bypass Angles in Order to Remove Lipid Accumulations in Atherosclerosis Disease by Simulation Method. Biosci Biotech Res Asia 2016;13(2). Available from: https://www.biotech-asia.org/?p=13710 |
Introduction
Aterosclerosis indication and clogged arteries especially in great and vital arteries lead to blood circulation system numerous disorders. Coronary arteries, carotid and femoral are the most important arteries that aterosclerosis speared in which could result in shock or heart attack (1). Recent studies for past decades revealed that in addition to physiological factors, inheritance, high lipid level of diet, obesity, diabetes, high blood pressure and smoking, hemodynamic factors influence disease indication significantly. Temporal and local fluctuations and also low scale of applied shear stress on arterial wall are among hemodynamic factors that affect disease development (2). Bypass surgical operation is a significant method to treat clogged arteries nowadays. Intimal hyperplasia phenomenon development threatens the success of following relationship: factors such as various flows inside the arteries including rotation, vortexes movement, shear stress distribution on arterial wall and etc. are all in association with this phenomenon (3). In US 30 to 60% of bypass grafting fail from 5 to 10 years and 15 to 30% of which lead to death. Bypass linkage technique, decision of bypass location, bad bypass design and etc. are among failure factors (4). Bypass construction should be designed as perfect as it would minimize flow turbulence. Numeral simulation techniques are advisable methods to achieve this purpose. Various studies have been applied to determine exact relationship between hemodynamic factors and disease progression, but due to multiplicity and/or unreal applied hypothesis significant success has not been obtained yet. Grafting angel effects and flow discharge in bypass branch location were studied by Fei et al. in 1994 (5). Hughes and How assessed geometrical effect of the model and flow division on flow pattern in bypass area (6). Ghalichi studied blood flow hemodynamic through numerical simulation of layer flows in low Reynolds numbers (7). Bali and Awasthi during studying on outside magnetic field on blood flow in thin arteries showed that resistance against the flow would increase if height raises and it would decrease if Hartmann number decreases (8). According to these studies it is revealed that upstream of bypass and clogged area is considered infrequently. Ogulu and Alabraba assessed affection of magnetic field movement on flow potential in arteries around the heart and heart itself (9). Ghaffari et al. evaluated the effect of magnetic field on plaque temperature distribution and realized that how it modifies plaque temperature and decrements it’s rupture probability (10). Sankar and Lee mathematically modeled non-Newtonian fluid impulse flow in narrow arteries (11). Tang et al. assessed blood impulse flow in three axial symmetric narrow tube models and three asymmetric narrow tubes with various narrowness intensity (12). According to these studies flow in the bypass accompanied artery is not considered and most of researchers considered blood as a Newtonian fluid and none has studied on magnetic field effect on bypass. We aimed to evaluate non-Newtonian fluid blood flow, permanently and non-permanently in clogged arteries and bypass effect on it and also in presence of magnetic field and gravity acceleration in different bypass angels. To achieve the purpose simulation of incompressible flow in three-dimensional spaces associated with equation of continuity solving and momentum and also coupling velocity amplitude and pressure with Rai and Chu method was accomplished.
Materials and Methods
Geometrical femoral bypass model: in this study a model of three-dimensional femoral artery with bypass and rigid wall was assumed (13). Percentages of blockage were 40%, 70% and 100%. Tow-dimensional geometry of the artery is shown in the figure 1.
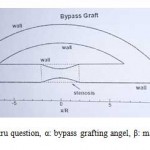 |
Figure 1: geometru question, α: bypass grafting angel, β: main artery angel. |
In this model α consisted of 30, 45 and 60 degrees. Β angel was assumed null. Percentages of blockage was defined as [(Ai – As)/Ai] in which Ai was non-blockage area, and As was the artery’s narrowest part area. In all cases distance between tow connection of 16R (R: artery radius) and 4R blockage length were considered. According to figure 1 in bypass geometry the blockage was located in the center. In 100% of blockage a total blockage was simulated by removing a part of the main artery.
In order to decrease time of computational calculations to stimulate the flow, unorganized networks were used for developing models networking. Desired geometry was modeled by SolidWorks software then networked in Gambit software. Network compression was enhanced by getting close to walls. Also in the location of grafting (bypass input and output) and blockage location (area contraction) network compression was utilized more (14). Figure 2 shows the sample of used network in following study.
 |
Figure 2: Used unorganized networks quality for femoral bypass. |
Equations and boundary conditions
Equation of the artery in the complete blockage area was as following:
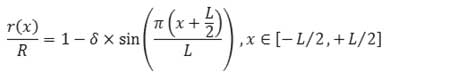 Equation 1
Equation 1
Equation of the artery in the blockage area. L: blockage length, δ: blockage maximum height.
Standard diameter of the artery was 0.0068m and bypass diameter was assumed similar to the artery’s. It has to be mentioned that in this study ideal geometry was used because lateral section of the artery was not a quit circle also it is variable along the artery. This simplifying indicated that in some arteries risks of re-obstruction are more than others.
In order to make an impulsive flow a sinusoidal relationship presented by deplane was used (equation 2) that had Reynolds mean of 230 and cardiac frequency period of 1 second. This relationship was chosen because of wide speared utilization for laboratorial and numeral approaches.
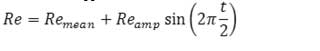 Equation 2
Equation 2
Sinusoidal relationship based on Reynolds number: Remean: moderate Reynolds number and Reamp: frequency amplitude of Reynolds number.
For the wall no slip boundary condition was applied. Due to cardiac frequencies translocation of artery was ignored. Artery wall was also considered impervious. In frequency condition because of velocity changing as the time changes in order to define the changes (figure 3), flow chart for a femoral artery that reveals of blood flow phase changing per time ratio was used. The flow was assumed calm and decompressed, stable and unstable impulsive, Newtonian and non-Newtonian. In Newtonian condition blood viscosity was constant and equal to 0.00345 P. in non-Newtonian condition for viscosity defining and shear ratio tow models of Cario were approached.
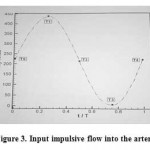 |
Figure 3: Input impulsive flow into the artery |
Blood was considered as electrical conductor fluid. Electromagnetic force that is produced via flow interaction with magnetic field was measured as follows: Fm= (J×B), J stands for flow density and B=B0+B1 were total magnetic field. B1 was induced magnetic field which was negligible in compression with outside magnetic field and could be ignored.
Fluid equation of continuity and momentum for analyzing the flow in presence of magnetic field and gravity acceleration were applied as follows:
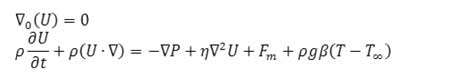 Equation 3
Equation 3
Fluid equation of continuity and momentum. U: velocity vector, P: pressure, ρ: density, η: fluid viscosity, g: gravity acceleration and β: Volume expansion coefficient.
Results
The effect of magnetic field from the outside: figure 4 shows the prophyl of axial velocity in bypass with 45°, 70% of obstruction, and Reynolds 250 for various amounts of hartmann number in tow sections. As the fluid moved from the wall toward the center of prophyl the velocity increased. After achieving to the maximum level it became sigmoid and went down to the axial (till it got null). Magnetic field induction led to blood axial velocity decrement. As Hartmann number rose under the affection of magnetic field, comparative velocity increased close to the walls and prophyl became more flat.
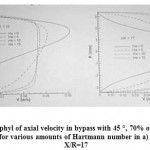 |
Figure 4. the prophyl of axial velocity in bypass with 45 °, 70% of obstruction, and Reynolds 250 for various amounts of Hartmann number in a) X/R=10 and b) X/R=17 |
Figure 5 shows shear stress in bottom of main artery wall with bypass angel of 45 ° and 70% obstruction for various amounts of Hartmann number and Reynolds 250. Figure 3 shows shear stress on the upper bypass wall under similar circumstance in Reynolds 400. Stress distribution has an important role to locate the plaques accumulation. Results revealed that induced magnetic force of blood flow acted as a resistant tensional force. Normal blood flow was the result of magnetic field thus outward viscosity was increased. In addition the effect of magnetic resulted in thickening boundary layer so as of velocity gradient increased close to the walls shear stress enhanced. In figure 2 when magnetic field is not applied due to positive pressure gradient negative shear stress in tow areas were observed. When magnetic field increased and Hartmann number enhanced subsequently there was no negative shear stress observation. In figure 3 in the bypass entrance there was returned flow, as the Hartmann number grew vortex power decreased so that in 10 and 20 Hartmanns returned flow was vanished completely.
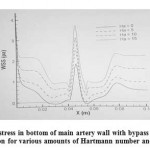 |
Figure 5: shear stress in bottom of main artery wall with bypass angel of 45 ° and 70% obstruction for various amounts of Hartmann number and Reynolds 250. |
Impulsive flow effect: when the frequencies of the heart cycle were considered, discharge frequent changes were observed that influenced other hemodynamic characteristics. As the results revealed in order to prevent temporary flow effects, approaching 3 cycles was necessary. In order to assess these frequencies, a heart cycle was segregated into some temporal stages. These temporal stages can be observed in table 4.
Table 4. A heart cycle stages scheduling (cycle 3).
| Stage | First | Second | Third | Fourth |
| Time | T1=2.25s | T2=2.5s | T3=2.75s | T4=3s |
| Description | Maximum discharge | Flow acceleration decrement | Minimum discharge | Flow acceleration |
| (Systole) | (abrupt drop) | (diastole) | (following cycle onset) |
In the table 5 maximum velocity in the focus of the blockage located in main artery central line for average Reynolds 230, bypass 45°, 70% of obstruction, for various times and in frequency range of 0.2, 0.4 and 0.6 are presented.
Table 5. Maximum velocity in the focus of the blockage located in main artery central line in various frequency times (m/s)
| t1=2.25s | t2=2.5s | t3=2.75s | t4=3s | |
| frequency range of 0.2 | 0.1725 | 0.1265 | 0.0888 | 0.137 |
| frequency range of 0.4 | 0.2111 | 0.1195 | 0.0425 | 0.1415 |
| frequency range of 0.6 | 0.2475 | 0.11 | 0.008 | 0.1473 |
Figure 6 presents shear stress in bottom wall of main artery for Reynolds 230, bypass 45°, 70% of obstruction, frequency range 0.2 in various times of the cycle. In t1 a strong vortex flow in downstream of the wall, was the main cause for severe drop of shear stress and becoming negative. Maximum shear stress in various times differed through the entrance velocity changes so it was enhanced by maximum shear stress increscent and vise versa.
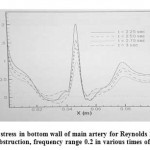 |
Figure 6: Shear stress in bottom wall of main artery for Reynolds 230, bypass 45°, 70% of obstruction, frequency range 0.2 in various times of the cycle |
Effect of gravity acceleration: results were assessed in four conditions by considering gravity acceleration; the first condition: the artery in horizontal position (Beta = 0°) and g = 0, the second condition: the artery in horizontal position (Beta = 0°) and g = -9.806m/s2, the third condition: the artery in vertical position (Beta = 90°) and g = -9.806m/s2 (blood flow against the gravity acceleration direction), the fourth condition: the artery in vertical position (Beta = 90°) and g = -9.806m/s2 (blood flow in the gravity acceleration direction)
Figure 7 shows the flow velocity in main artery central line of the blockage location for average Reynolds 125, bypass 45° and 40% of obstruction. According to the figure in the first condition the maximum velocity in the blockage was 0.11137 m/s and also in this condition in the presence of gravity acceleration (the second condition) it rose up to 0.1174 m/s. in the third condition as the flow went up maximum velocity became 0.10614 m/s. in the fourth condition fluid velocity under the affection of gravity grew to 0.1206 m/s. Generally mean of velocity in the central line of the main artery from the first condition to the second condition 2.47% and from the third condition to the fourth condition 16.7% increased. For the shear stress in general the mean increased 4.4% from the first condition to the second condition, 43.2% from the first condition to the third condition and decreased 48.2% and 63.8% from the first condition to the fourth condition and from the third condition to the fourth condition in order. This revealed of the gravity acceleration importance especially in the third and fourth conditions.
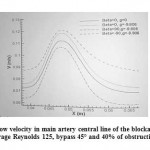 |
Figure 7: The flow velocity in main artery central line of the blockage location for average Reynolds 125, bypass 45° and 40% of obstruction |
Discussion and Conclusion
The effect of the magnetic field from the outside: during wide speared investigations on biological fluid dynamic in the presence of magnetic field it has been revealed that blood as a biological fluid has a magnetic conduct. This feature has been referred to intra cellular proteins, cell membrane and hemoglobin as a type of iron oxide. When blood as a magnetic fluid exposes to a magnetic field it gains magnetic rotation. The amount of blood burden in association with magnetic field leads to suspension of red blood cells in plasma and hemoglobin concentration increscent thus blood concentration rises up and subsequently blood velocity decreases. According to that of increasing of Hartmann number causes flattening velocity prophyl, as it increases comparative velocity rises close to the walls. Totally applied magnetic force acts as a resistant tensional force that leads to increscent of outward viscosity, decreasing of boundary layer thickness and enhancement of velocity gradient close to the walls which causes shear stress increscent. These results confirmed previously reports (8, 15). Ghafari et al. despite of considering blood as Newtonian fluid, obtained results compliant to ours (10). They reported that choosing appropriate direction for magnetic field in the best choice to decrease the probability of artery rupture.
Effect of impulsive flow: when the heart cycle frequencies were considered frequent changes of discharge was observed which affect other hemodynamic features. Results indicated that as of frequency amplitude increscent in maximum discharge velocity increased and in minimum discharge it decreased. Sankar presented a developed analysis of impulsive flow affection by a turbulence method that via associating their results with ours it is concluded that for every value of index, in some points of the pulse which the velocity was high, maximum shear stress increased and vice versa (in some points of the pulse with a low velocity, maximum shear stress was decreased). These results revealed that impulsive flow can cause returned flow (in maximum discharge) after the obstruction which calculating the amounts seems to be necessary to optimize bypass surgical operations (16).
The effect of gravity acceleration: by considering the term of the gravity acceleration bypass surgical operations could be helped. The mean of shear stress when the flow moves against the gravity direction was more than when it moves in the same direction of the gravity acceleration, however when the flow is aligned with gravity returned flow is observed. Therefore it is concluded that bypass surgical operation for arteries that the flow in which is against the gravity acceleration direction is more appropriate. Gyordana and et al report in 2005 was one of negligible studies that were applied in this field in which they have obtained similar results (17).
In conclusion calculation of all hemodynamic parameters and affecting environmental factors on them including magnetic field, impulsive flow and gravity acceleration are necessary on improving the efficiency of bypass surgical operations. If the three-dimensional modeling approaches maximally match with the reality they could help the specialists to choose the best location and angel of the bypass and improve the achievement probability significantly. Hence it seems that keen calculation of impulsive flow and induction of magnetic field for short period and also evaluating the effect of gravity force on the location of the bypass for a long time is crucial for this surgical operation success.
References
- Herisson F, Heymann M-F, Chétiveaux M, Charrier C, Battaglia S, Pilet P, et al. Carotid and femoral atherosclerotic plaques show different morphology. Atherosclerosis. 2011;216(2):348-54.
- Yamauchi H, Nishii R, Higashi T, Kagawa S, Fukuyama H. Hemodynamic compromise as a cause of internal border-zone infarction and cortical neuronal damage in atherosclerotic middle cerebral artery disease. Stroke. 2009;40(12):3730-5.
- Stefanidis D, Kuwada TS, Gersin KS. The importance of the length of the limbs for gastric bypass patients—an evidence-based review. Obesity surgery. 2011;21(1):119-24.
- Parikh DS, Swaminathan M, Archer LE, Inrig JK, Szczech LA, Shaw AD, et al. Perioperative outcomes among patients with end-stage renal disease following coronary artery bypass surgery in the USA. Nephrology Dialysis Transplantation. 2010:gfp781.
- Fei D-Y, Thomas JD, Rittgers SE. The effect of angle and flow rate upon hemodynamics in distal vascular graft anastomoses: a numerical model study. Journal of biomechanical engineering. 1994;116(3):331-6.
- Hughes P, How T. Effects of geometry and flow division on flow structures in models of the distal end-to-side anastomosis. Journal of biomechanics. 1996;29(7):855-72.
- Ghalichi F. Pulsatile laminar and turbulent blood flow simulation in large stenosed arteries and stenosed carotid artery bifurcation1999.
- Bali R, Awasthi U. Effect of a magnetic field on the resistance to blood flow through stenotic artery. Applied Mathematics and Computation. 2007;188(2):1635-41.
- Ogulu A, Alabraba M. Magnetic effect on low Reynolds number flow in a heated tube of slowly varying section. Acta Physica Hungarica. 1992;72(2-4):223-34.
- Ghaffari S, Alizadeh S, Karimi M. Effect of magnetic field on temperature distribution of atherosclerotic plaques in coronary artery under pulsatile blood flow condition. International Journal of Thermal Sciences. 2013;64:40-52.
- Sankar D, Lee U. Mathematical modeling of pulsatile flow of non-Newtonian fluid in stenosed arteries. Communications in Nonlinear Science and Numerical Simulation. 2009;14(7):2971-81.
- Tang D, Yang C, Kobayashi S, Ku DN. Steady flow and wall compression in stenotic arteries: a three-dimensional thick-wall model with fluid–wall interactions. Journal of biomechanical engineering. 2001;123(6):548-57.
- Longest PW, Kleinstreuer C. Particle-hemodynamics modeling of the distal end-to-side femoral bypass: effects of graft caliber and graft-end cut. Medical engineering & physics. 2003;25(10):843-58.
- c Wilson KW, Dutton RW, Taylor C, editors. A Software Framework for Creating Patient Specific Geometric Models from Medical Imaging Data for Simulation Based Medical Planning of Vascular Surgery. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2001: 4th International Conference Utrecht, The Netherlands, October 14-17, 2001 Proceedings; 2003: Springer.
- Varshney G, Katiyar V, Kumar S. Effect of magnetic field on the blood flow in artery having multiple stenosis: a numerical study. International Journal of Engineering, Science and Technology. 2010;2(2):967-82.
- Ojha M, Cobbold RS, Johnston KW, Hummel RL. Pulsatile flow through constricted tubes: an experimental investigation using photochromic tracer methods. Journal of fluid mechanics. 1989;203:173-97.
- Giordana S, Sherwin S, Peiró J, Doorly D, Crane J, Lee K, et al. Local and global geometric influence on steady flow in distal anastomoses of peripheral bypass grafts. Journal of biomechanical engineering. 2005;127(7):1087-98.

This work is licensed under a Creative Commons Attribution 4.0 International License.





