How to Cite | Publication History | PlumX Article Matrix
A Novel Approach on Discrete Cosion Transform Based Image Compression Technique for Lung Cancer
T. Karthikeyan1 and C. Thirumoorthi 2*
1Department of Computer Science, PSG College of Arts and Science, Coimbatore, India.
2Research Scholar, Bharathiar University, Coimbatore, Department of Computer Science, Hindustan College of Arts and Science, Coimbatore, India.
Corresponding Author E-mail: cthirumoorthymca@gmail.com
DOI : http://dx.doi.org/10.13005/bbra/2317
ABSTRACT: In medical field the volume of medical image data produced every day is ever growing, particularly in grouping with the improved scanning resolutions and the importance of volumetric medical image data sets. In this work, five image compression methods are simulated. They are Karhunen-Loève Transform (KLT), Walsh-Hadamard Transform (WHT), Fast Fourier Transform (FFT), proposed Sparse Fast Fourier Transform (SFFT) and Discrete Cosine Transform (DCT). The results of simulation are shown and compared different quality parameters of it are by applying on various lung cancer CT Scan medical images. The DCT method algorithm was given better results like Compression Ratio (CR), Structural Content (SC), Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) compare to other Transform methods. The DCT technique given improved result compared with other methods in all evaluation measures.
KEYWORDS: Image compression; KLT; WHT; FFT; SFFT; DCT; lung cancer CT images; CR; SC; MSE; PSNR
Download this article as:| Copy the following to cite this article: Karthikeyan T, Thirumoorthi C. A Novel Approach on Discrete Cosion Transform Based Image Compression Technique for Lung Cancer. Biosci Biotech Res Asia 2016;13(3). |
| Copy the following to cite this URL: Karthikeyan T, Thirumoorthi C. A Novel Approach on Discrete Cosion Transform Based Image Compression Technique for Lung Cancer. Biosci Biotech Res Asia 2016;13(3). Available from: https://www.biotech-asia.org/?p=15521 |
Introduction
The health care field have large amount of medical images. So they need decrease the large volume amount of medical images. The Image compression is a process that focused on decreasing the size without losing quality, decrease the storage space of images and information of image. Lung cancer is the most common cause of cancer death in the world. Tobacco smoking cause’s etiology breath and lung cancer. Patients at highly effected by the lung cancer [1]. It’s could present with a variety of indications and is regularly screened by more common sicknesses. Several patients report no indications what so always, so it is vital that exact questions be enquired to try to produce info about symptoms they may not reflect abnormal[2]. In the case of an abnormal chest x-ray, the patient should directly undergo a chest CT scan for further evaluation. Figure 1 shows that the unusual lung CTs inpatients who originally obtainable with weight loss and cough. The positron emission tomography was clarifying that the extent of the cancer [3]. When lung cancer is assumed, the patient stated to an oncologist, who will decide the supreme suitable diagnostic process (e.g., bronchoscopy, CT guided lung biopsy, sputum cytology or media stinoscopy) and utmost favorable whole course of therapy for the lung cancer patient’s specific needs. The image compression techniques like KLT, WHT, FFT, SFFT and DCT were used to compress the lung cancer CT scan medical images. Anamitra Bardhan Roy discussed comparison of FFT, DCT, DWT, WHT Compression Techniques. Walaa M. Abd-Elhafiez et.al said the compression analysis results have indicated that the performance of the suggested method is much better, where the constructed images are less distorted and compressed with higher factor.
The actual context that determines when to use lossless versus lossy compression and the actual parameters for tweaking the compression system are left to the judgment of the implementer and the use case. Compression standards, such as JPEG or JPEG-LS, have a very limited set of options regarding their setup. Harjeet pal singh et.al defined compression is reducing the size of graphics file, without compromising on its quality.
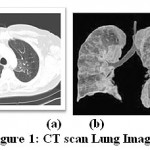 |
Figure 1: CT scan Lung Image
|
Image Compression Methodology
Image compression is process to remove the redundant information from the image so that only essential information can be stored to reduce the storage size, transmission bandwidth and transmission time[4][5]. Figure 2 shows that the essential information is extracted by various transforms techniques such that it can be reconstructed without losing quality and information of the image[6][7][8]. In this work comparative analysis of image compression is done by seven transform methods[9][10][11], which are Karhunen-Loève Transform (KLT), Walsh-Hadamard Transform (WHT), Fast Fourier Transform (FFT), proposed Sparse Fast Fourier Transform (SFFT) and Discrete Cosine Transform (DCT).
Karhunen-Loève Transform (KLT)
Hotelling transform also known as Karhunen-Loève Transform or KLT, minimizes MSE that is present between original (sub) image and (decompressed) reconstruction[12][13]. Thus for any image KLT is the optimal information compaction transformation as well as for any number of retained coefficients. KLT basic functioning is dependent on image but, this however makes pre-computing impossible and hence this does not qualify it as a practical option suitable for image compression.
There are several applications where KLT [14] has been widely used as in multi-spectral analysis of satellite-gathered images through the resulting spectral signature of imaged regions. Also there is significant data reduction that is attained while storing satellite images considering multi-spectral sets have been transformed to KLT space. Recently KLT has been used to facilitate images in facial recognition[15]. It is important to note that image set size is possibly much bigger in the subsequent two applications.
 |
Figure 2: Compression Techniques
|
Let us take into consideration a sample set of real-valued images from an ensemble of images[16]. Create vectors with the equivalent pixel taken from each of the images, i.e. if there are D images each of size then form the column vectors
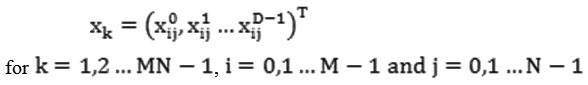
(with superscript T representing the transpose). Calculate the sample mean vector using the formula
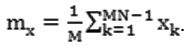
Use a computational formula to create the sample covariance matrix as
![]()
where {uk} are the eigenvectors with associated eigenvalue set{λk}. The KLT kernel is a unitary matrix, [V], whose columns,{uk} (arranged in descending order of eigenvalue amplitude), are used to transform each zero-meaned vector:
![]()
Walsh-Hadamard Transform (WHT)
Walsh system functions forms the very basis for Walsh transform. Walsh functions are orthogonal and have only +1 and -1 values [17]. In general, the Walsh transform can be generated by the Hadamard matrix as follows:
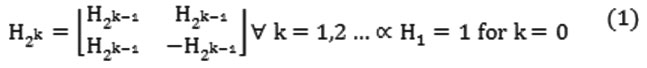
WHT here was employed to facilitate face as well as signature [18][19] recognition
as WHT coefficients output array comprises only of integer values, resultantly Hadamard transform thus becomes a quick transform, and implementation is feasible in O (N log N) additions as well as subtractions.
Fourier Transform
Fourier Transform is known to decompose image as two components: sinus and cosines. This implies that FT will transform any image from spatial to frequency domain respectively [20]. Fact is that any function can be precisely approximated using sum of infinite sinus and cosines functions [21]. Fourier Transform essentially is a method to execute this. Mathematically a two dimensional images Fourier transform is:
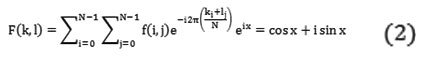
Here is the image value in its spatial domain and F in its frequency domain. Transformation results in complex numbers. This can be showing either using a real and complex image or using a magnitude and phase image [22]. Though, in image processing algorithms it the magnitude image alone which is of interest as it has the information required regarding the geometric structures of the images. Nonetheless, in case there is a necessity to modify image in the particular forms what is required to retransform is the need to preserve both.
Fast Fourier Transform
The Fast Fourier Transform (FFT) algorithm was established by Carl Friedrich Gauss nearby 1805. The FFT is used to compute the Discrete Fourier Transform (DFT). The bigger size M = NxN matrix split into smaller size N’s of DFT in the time domain. The new Radix-2 Decimation in Time (DIT) FFT is the effective and simplest method. It’s also used to compute 2n point DFT. In the FFT method the given weights are multiplied by indexes. The output should be the bit reverse form of the given input signal. The compound conjugate regularity is used to signify the imaginary part.
Methodology (Sparse Fast Fourier Transform – sFFT)
For any algorithms which is used to compute DFT must take time at least proportional to its output size, Ω(n). Most of the signals in frequency domain are sparse[23]. In general signal processing techniques many applications contain small value of Fourier coefficients or equal to zero. So the resultant DFT is approximately sparse. This is general in video, that is most of the coefficient are negligible. Images and videos are equally sparse[24]. An efficient algorithm is needed to compute FFT for the signals that are sparse in frequency domain. sFFT computes k – sparse approximation, whose runtime depends upon k, the larger coefficient in the signal. This algorithm works in the process of identifying these k values by a filter G. G concentrates in both time and frequency. G is zero for all values except at a small number of time co-ordinates, and the Fourier Transform of G ( is negligible except at a small fraction value which is about of the frequency co-ordinates [25]. Gaussian or Dolph-Chebyshev function convolved with a box-car function is used to identify the large coefficients in sFFT. Using this filter to find location and magnitude of the higher frequency component, parallel acceleration is achieved easily [26] .
Previous sub-linear algorithms have a runtime which is a polynomial in k and log n3. The fastest runtime of these algorithms will be
![]()
For some constants C>2.
The key feature of sFFT is its simple structure. It has an efficient runtime with low big- 0th Constant. For a typical case of n which is a power of 2, the run time is

The implementation method and the working of sFFT with mathematical derivative. The research is made with 128×128 medical image to compression and decompression with KLT, WHT, FFT and Proposed sFFT and calculating PSNR, MSE, CR, SC [27].
sFFT Algorithm.
The structure of the proposed method contains following steps:
The research is made with FFT to compute the Fourier Transform in a MATLAB application.
The execution of the FFT algorithm in MATLAB application.
The research is made with SFFT to compute the Fourier Transform in a single array.
The execution of the SFFT algorithm Coding is based on Matlab library function and header files.
The development and implementation of SFFT algorithm for computing DFT should be Ykj
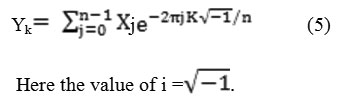
Discrete Cosine Transform
The Discrete Cosine Transform (DCT) is an orthogonal transform, its attempts to the de-correlate the medical image data. After the de-correlation each transform coefficient can be independently encoded without losing the compression efficiency [28]. The DCT transforms the signal from the spatial representation into the frequency representation. The DCT signify an image as a summation of sinusoids of the varying magnitudes and frequencies. DCT property is a typical image utmost of the visually substantial information about an image is focused in just few coefficients of DCT. Afterwards the computation of the DCT coefficients, they are regularized according to a quantization table with the different measures provided by the JPEG image standard computed by the psycho visual evidence. The Selection of quantization table affects the compression ratio and entropy. The value of quantization is inversely proportional to quality of reconstructed image. Its gives better compression ratio and better mean square error [29]. In a Quantization, the less significant frequencies are discarded, and then the maximum important frequencies that remain are used to recover the image in decomposition method. After quantization, the quantized coefficients are rearranged in the zigzag order for the further compressed by an effective lossy coding algorithm. DCT has several merits: (1) It has the ability to pack more information in least coefficients. (2) It decreases the block like appearance called the blocking artifact that outputs when margins between sub-images become visible [30].
An image is signified as the two dimensional matrix, the 2-D DCT is used to compute a DCT Coefficients of an image. The 2-D DCT for an NXN input order can be defined as follows [31]:
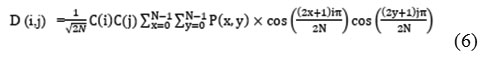
Where, P(x, y) is the input matrix image NxN, (x, y) are the coordinate of the matrix elements and (i, j) are the coordinate of the coefficients, and
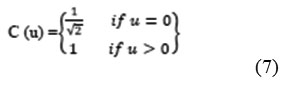
The reconstructed image is the computed by using the inverse DCT (IDCT) according to the
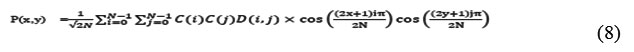
The black and white image pixels are ranged from 0 to 255, where 0 matches to pure black and 255 matches to a pure white. As DCT is constructed to work on pixel the values ranging from -128 to 127, the original block is the level off by 128 from every entry [32]. The Step by step Procedure of getting compressed image is using DCT and getting reconstructed image from the compressed image.
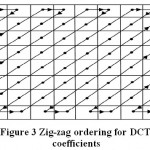 |
Figure 3: Zig-zag ordering for DCT coefficients
|
Currently encoding is completed and transmitted to receiver side in the form of the one dimensional array. This transmitted order saves in the text format. The array of compressed blocks that establish the image is stored in a extremely reduced amount of the space. Further the compression can be reached by applying suitable scaling factor [33]. In order to rebuild the output data, the rescaling and the de-quantization should be achieved as given in Equation.
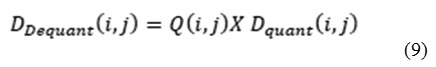
The de-quantized matrix is then transmuted back using the 2-D inverse-DCT [34]. The equation for the 2-D inversed DCT change is given in the above said Equation.
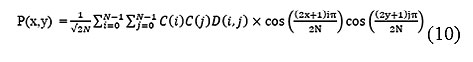
DCT separates images into the parts of different frequencies where less important frequencies are the discarded through quantization and important frequencies is used to retrieve to the image through decompression.The following equation is given by the forward 2D_DCT transformation:
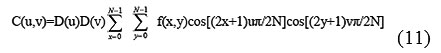
Where u,v =0,1,2,3,……………,N-1
The following equation is given by the inverse 2D-DCT transformation:
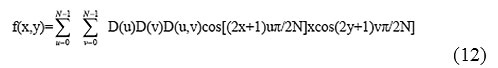
where
D(u)=(1/N) ^1/2 for u=0
D(u)=2(/N)^1/2 for u=1,2,3…….,(N-1)
Compared to the other input dependent transforms, DCT have several advantages: (1) It have been implemented in single combined circuit; (2) It has the capability to pack most info in fewest coefficients; (3) It reduces the block like appearance so-called blocking artifact that results when limits between sub-images convert visible[35][36][37].
Performance Evaluation
Peak Signal to Noise Ratio (PSNR in dB)
PSNR called as Peak Signal-to-Noise Ratio. PSNR approximates image quality index, however on its own it does not have the capability of drawing a comparison between the features of two distinct images [38][39]. There is a possibility however that lower PSNR image may be considered as an image whose tone quality is comparatively better than one with a higher signal to noise ratio [40].
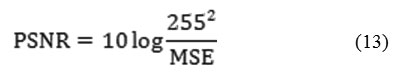
Its refers to the relation between the power of the humiliating noise that affects the loyalty of its representation and the supreme imaginable power of the signal [41]. As several signals inherently have an extensive dynamic range, PSNR generally is expressed as logarithmic decibel scale.
Mean Square Error (MSE)
Mean square error is a measure of image quality index. Large value of mean square basically implies that a poor quality image [42]. Mean Square Error called as MSE. Generally, it is a criterion that has been widely used and is representative of the classical error estimate as denoted by equation below:
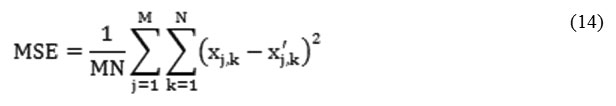
where M and N are the image dimensions.
Compression Ratio (CR)
Compression Ratio is the ratio of number bits required to represent the data before compression to the number of bits required to represent data after compression [43]. Increase of compression ratio causes more effective compression technique employed and vice versa [44].
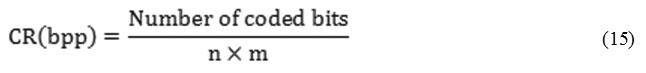
Structural Content (SC)
Structural content measure that is employed to draw a comparison between two images inherent in several small image patches and to determine the images have in common [45][46]. A comparison is drawn between patches by deploying 2D continuous wavelet that acts as a low level corner detector[47][48]. Large value of structural content SC basically implies a poor quality image [49].
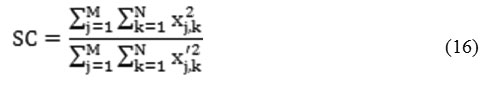
Experimental Results and Discussions
The experiment is carried out in MATLAB environment. In this research, the images deployed here for compression are all 128 X 128, 8-bit medical images. Basically meaning that images comprise of 128 X 128 = 16,384 pixels, wherein each pixel is represented by 8 bits or 1 byte. KLT, WHT, FFT, SFFT and DCT algorithm implementation has been carried out on MATLAB software and several different parameters have been ascertained with respect to the three medical images; comparison of reconstructed and original images PSNR, MSE, CR, SC values have been estimated.
In Table-1 we have taken 128X128 size three CT medical images and simulated images using KLT, WHT, FFT , SFFT and DCT compression techniques. In first CT Image gave good result in DCT for PSNR value is 38.9746 less than KLT, WHT, FFT and SFFT value is 43.3436, 41.0181 ,40.7637 and 39.7656 respectively. In second CT Image gave good result in DCT for PSNR value is 40.6542 less than KLT, WHT , FFT and SFFT value is 51.9335, 48.5279, 44.6743 and 42.3932 respectively. In third CT Image gave good result in DCT for PSNR value is 38.8023 less than KLT, WHT, FFT and SFFT value is 52.8757, 50.6854 , 47.9874 and 45.0043 respectively.
In first CT Image gave good result in DCT for MSE value is 14.424 higher than KLT, WHT, FFT and SFFT value is 2.342, 3.165, 8.437and 10.373 respectively. In second CT Image gave good result in DCT for MSE value is 16.232 higher than KLT, WHT , FFT and SFFT value is 7.0676, 9.9067, 10.0932 and 12.3254 respectively. In third CT Image gave good result in DCT for MSE value is 19.313 higher than KLT, WHT, FFT and SFFT value is 6.874, 7.429 , 10.453 and 12.842 respectively.
In first CT Image gave good result in DCT for value CR is 5.9784 higher than KLT, WHT, FFT and SFFT value is 2.6822, 3.7365, 4.4844 and 5.3433 respectively. In second CT Image gave good result in DCT for CR value is 4.985 higher than KLT, WHT , FFT and SFFT value is 1.369, 2.9231, 3.242 and 4.043 respectively. In third CT Image gave good result in DCT for CR value is 6.382 higher than KLT, WHT, FFT and SFFT value is 2.836, 3.1302, 4.043 and 5.132 respectively.
In first CT Image gave good result in DCT for value SC is 2.105 less than KLT, WHT, FFT and SFFT value is 3.984, 3.098, 2.965 and 2.615 respectively. In second CT Image gave good result in DCT for SC value is 2.816 less than KLT, WHT, FFT and SFFT value is 4.534, 4.053, 3.785 and 3.166 respectively. In third CT Image gave good result in DCT for SC value is 2.008 less than KLT, WHT, FFT and SFFT value is 3.723, 3.108, 2.768 and 2.564 respectively.
In Figure-4, Figure-5, Figure-6 , Figure-7 charts and Table -1 explained the PSNR, MSE, CR and SC parameters.
The DCT method gave less SC value are given three CT image. Also it produced high MSE and CR Value compare to the other exiting methods. It also shows in Figure-3, Figure-4, Figure-5 , Figure-6 and Figure-7.
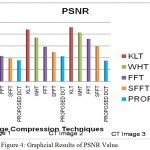 |
Figure 4: Graphcial Results of PSNR Value.
|
 |
Figure 5: Graphcial Results of MSE Value.
|
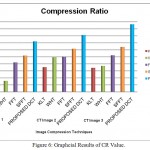 |
Figure 6: Graphcial Results of CR Value.
|
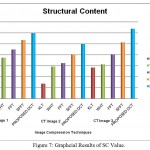 |
Figure 7: Graphcial Results of SC Value.
|
Table 1: Medical image encoding is simulated by using CT images of size 128X 128 with different compression techniques like KLT, WHT, FFT, SFFT and DCT.
| Medical Image | Image compression Technique Used | PSNR | MSE | CR | SC |
| CT IMAGE 1 | KLT | 43.3436 | 2.342 | 2.6822 | 3.984 |
| WHT | 41.0181 | 3.165 | 3.7365 | 3.098 | |
| FFT | 40.7637 | 8.437 | 4.4844 | 2.965 | |
| SFFT | 39.7656 | 10.373 | 5.3433 | 2.615 | |
| PROPOSED DCT | 38.9746 | 14.424 | 5.9784 | 2.105 | |
| CT IMAGE2 | KLT | 51.9335 | 7.0676 | 1.369 | 4.534 |
| WHT | 48.5279 | 9.9067 | 2.9231 | 4.053 | |
| FFT | 44.6743 | 10.0932 | 3.242 | 3.785 | |
| SFFT | 42.3932 | 12.3254 | 4.043 | 3.166 | |
| PROPOSED DCT | 40.6542 | 16.232 | 4.985 | 2.816 | |
| CT IMAGE 3 | KLT | 52.8757 | 6.874 | 2.836 | 3.723 |
| WHT | 50.6854 | 7.429 | 3.1302 | 3.108 | |
| FFT | 47.9874 | 10.453 | 4.043 | 2.768 | |
| SFFT | 45.0043 | 12.842 | 5.132 | 2.564 | |
| PROPOSED DCT | 38.8023 | 19.313 | 6.382 | 2.008 |
Conclusion
This paper is focused on the comparison among four important KLT, WHT, FFT ,SFFT and DCT methods of image compression. In this paper analysis of various Image compression methods for different images is done based on parameters, mean square error (MSE), compression ratio(CR), and peak signal to noise ratio (PSNR). The comparison of KLT, WHT, FFT , SFFT and DCT after compression the parameters like PSNR values, MSE, CR and SC values were good outcome in proposed DCT work. From the above study it can be seen that Proposed DCT take less PSNR value and SC value than KLT, WHT, FFT and SFFT. The Proposed method has more compression ratio and MSE than KLT, WHT , FFT & SFFT. Our simulation results from result and discussion chapter shows that we can achieve higher compression ratio using DCT compression technique. DCT transform gives higher compression ratio but for getting that clarity of the image is partially trade off. It is more suitable for regular applications as it is having a good compression ratio along with preserving most of the information.
Future Work
The result in this paper provides a strong foundation for future work for the compression method. All of the analysis presented in this paper work involved exhaustive simulations using 128X128 pixel medical images, in future we take 256X256 pixel medical images and 512X512 pixcel medical images . The algorithm can be realized in hardware and software implementation as a future work. It can also be a good choice for the image processor of the transform system. This research work has been analysed for high compression ratio. Further research work can be performed to relax high compression ratio constraint and transform. This work has been concentrate transform image using for the elimination of the spatial redundancy by DCT compression of medical images.
References
- Fukuoka M, Yano S, Giaccone G, Tamura T, Nakagawa K, Douillard JY, Nishiwaki Y, Vansteenkiste J, Kudoh S, Rischin D and Eek R. Multi-institutional randomized phase II trial of gefitinib for previously treated patients with advanced non–small-cell lung cancer. Journal of Clinical Oncology, 2003; 21(12): 2237-2246.
CrossRef - Pretreatment Evaluation of Non–Small-cell Lung Cancer, American Journal of Respiratory and Critical Care Medicine, Vol. 156, No. 1 (1997), pp. 320-332.
CrossRef - Halpern MT, Gillespie BW and Warner KE. Patterns of absolute risk of lung cancer mortality in former smokers. Journal of the National Cancer Institute, 1993; 85(6): 457-464.
CrossRef - Mohammed AA, Hussein JA., Hybrid transform coding scheme for medical image application. In IEEE ISSPIT 10’, 2010; 237-240.
CrossRef - Zhang SQ, Zhang SF, Wang XN, Wang Y. The Image Compression Method Based on Adaptive Segment and Adaptive Quantified. In IEEE 3rd ICICIC’08, 2008; 353-353.
CrossRef - Lewis and G. Knowles, ―Image compression using the 2-D wavelet transforms,IEEE Trans. Image Processing, vol. 1, pp. 244-250, April 1992.
CrossRef - Averbuch A., Lazar Danny and Israeli Moshe, ―Image Compression using WT and Multiresolution Decomposition‖, IEEE Trans. On Image Processing. Vol. 5, No. 1 (1996) , Jan 31.
- Ghanbari “Standard Codecs: Image Compression to Advanced Video Coding” Institution Electrical Engineers, ISBN: 0852967101, 2003.
- Furht, B. (1998) ―Image Presentation and Compression‖, chap. 8. CRC Press, Inc., 1st edn.
- Singh, V. Kumar, and H. K. Verma, ―DWT-DCT hybrid scheme for medical image compression, Medical Engineering and Technology, vol. 31, pp. 109–122, 2007.
CrossRef - Gonzalez, R. and Eugene, R. ―Digital image processing, 2008.
- Thyagarajan, S.K. ―Still image and video compression with Matlab‖, 2007.
CrossRef - Yun Q. Shi and Huifang Sun. ―Image and Video Compression for Multimedia Engineering: Fundamentals, Algorithms, and Standards‖. CRC Press LLC, Boca Raton FL, first edition, 2000.
- Gerbrands, Jan J, On the relationships between SVD, KLT and PCA, Pattern recognition 14.1:375-381, 1981
CrossRef - Xie Y, Jing X, Sun S, Hong L. A fast and low complicated image compression algorithm for predictor of JPEG-LS. In IEEE IC-NIDC, 2009; 353-356.
- Thirumoorthi C, Karthikeyan T, A Review on Embedded Zero Wavelet Transform Coding, in Proceedings of National conference on Advanced Trends in Information Technology (NCATIT -2016). ISBN 938054317-4. Souvenir Page.No:40.
- Wei L., Research on Image Compression Algorithm Based on SPHIT. In 3rd IEEE ICINIS, 2010; 104-107.
- Muhammad Azhar Iqbal, Dr Muhammad Younus Javed, Usman Qayyum, ―Curvelet-based Image Compression with SPIHT‖, IEEE computer society. International Conference on Convergence Information Technology, 2007.
- Mridul Kumar Mathur, Gunjan Mathur, Image Compression using DFT through Fast Fourier Transform Technique, International Journal of Emerging Trends & Technology in Computer Science (IJETTCS), volume 1, Issue 2, July – August 2012.
- Roy AB, Dey D, Mohanty B and Banerjee D. Comparison of FFT, DCT, DWT, WHT Compression Techniques on Electro cardiogram & Photo plethy smography Signals, Anamitra Bardhan Roy -Special Issue of International Journal of Computer Applications (0975 – 8887) International Conference on Computing, Communication and Sensor Network (CCSN) 2012.
- Walaa M. Abd-Elhafiez, Wajeb Gharibi, Color Image Compression Algorithm Based on DCT Blocks, International Journal of Computer Science Issues, IJCSI, vol. 9, Issue 4, July 2012, pp. 323-328.
- Singh H, Sharma S., Hybrid Image Compression Using DWT, DCT & Huffman Encoding Techniques. International Journal of Emerging Technology and Advanced Engineering, 2012; 2(10): 300-306.
- Anoop Mathew and Bensiker Raja Singh D, ―Image Compression using Lifting based DWT‖, International Journal of computers, Information Technology and Engineering, Jan-June 2009.
- Elharar, Adrian Stern, OferHadar,“A Hybrid Compression Method for Integral Images Using Discrete Wavelet Transform and Discrete Cosine Transform”, Member, IEEE, and Bahram Javidi, Fellow, IEEE.
- B, Thiyagarajans. S, ―Hybrid Transformation technique for image compression‖,Journal of theoretical and applied information technology, 31st July 2012 Vol. 41 No.2.
- Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, Image quality assessment: From error visibility to structural similarity, IEEE Trans. on Image Processing, vol. 13, no. 4, pp. 600-612, Apr. 2004.
CrossRef - Harjeet pal singh, Sakhi Sharma, Hybrid Image Compression Using DWT, DCT & Huffman Encoding Techniques International Journal of Emerging Technology and Advanced Engineering, (ISSN 2250-2459, Volume 2, Issue 10, October 2012.
- Al-Fayadh A, Hussain AJ, Lisboa P, Al-Jumeily D. An adaptive hybrid classified vector quantisation and its application to image compression. In IEEE Computer Modeling and Simulation EMS’08. 2008; pp. 253-256.
- Shrestha S, Wahid K. Hybrid DWT-DCT algorithm for biomedical image and video compression applications. In IEEE 10th ICISSPA, 2010; 280-283.
CrossRef - Roy AB, Dey D, Mohanty B and Banerjee D. Comparison of FFT, DCT, DWT, WHT Compression Techniques on Electrocardiogram and Photoplethysmography Signals. In IJCA Special Issue on International Conference on Computing, Communication and Sensor Network CCSN, 2012; 6-11.
- T.Karthikeyan, C.Thirumoorthi Embedded zero tree Wavelet (EZW) Algorithm based Image Transformation for Easy Optimization with HALIDE Language, International Journal of Applied Engineering Research (IJAER), ISSN 0973-4562 Vol. 10 No.55 (2015) , Page No 1551-1554, June- 2015 .
- Yun Q. Shi and Huifang Sun. ―Image and Video Compression for Multimedia Engineering: Fundamentals, Algorithms, and Standards‖. CRC Press LLC, Boca Raton FL, first edition, 2000.
- T. Karthikeyan & C.Thirumoorthi. Easy Optimization of Image Transformation using sFFT Algorithm with HALIDE Language, in International Conference on “Contemporary Computing and Informatics (IC3I 2014)”, Proceedings published in IEEE xplore, Pages: 1188 – 1190 (2014), ISSN: 978-1-4799-6629-5/14.
- Anoop Mathew and Bensiker Raja Singh D, ―Image Compression using Lifting based DWT‖, International Journal of computers, Information Technology and Engineering, Jan-June 2009.
- T.Karthikeyan & C.Thirumoorthi. A Survey on Embedded Zero Tree Wavelet, International Journal of Computer Science (IJCS), ISSN: 2348-6600, Vol.2, Issue 2, No:3, Ref-ID: IJCS-061, Page No:353-357, October- 2014.
- Lewis and G. Knowles, ―Image compression using the 2-D wavelet transforms,IEEE Trans. Image Processing, vol. 1, pp. 244-250, April 1992.
CrossRef - Averbuch A., Lazar Danny and Israeli Moshe, ―Image Compression using WT and Multiresolution Decomposition‖, IEEE Trans. On Image Processing. Vol. 5, No. 1 (1996) , Jan 31.
- Furht, B. (1998) ―Image Presentation and Compression‖, chap. 8. CRC Press, Inc., 1st edn.
- Richardson, I. E. (2002) ―Video Codec Design: Developing Image and Video Compression Systems‖. John Wiley & Sons, Inc.
CrossRef - Salomon, D. (2004) Data Compression: ―The Complete Reference‖ third edn.
- Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004) Image quality assessment: from error visibility to structural similarity. Image Processing, IEEE Transactions.
- Singh, V. Kumar, and H. K. Verma, ―DWT-DCT hybrid scheme for medical image compression, Medical Engineering and Technology, vol. 31, pp. 109–122, 2007.
CrossRef - Gonzalez, R. and Eugene, R. ―Digital image processing , 2008.
- Thyagarajan, S.K. ―Still image and video compression with Matlab‖, 2007.
- Chuanwei Sun 1Quanbin Li, Jingao Liu ―The Study of Digital Image Compression Based on Wavelets‖, ICALIP2010.
- Anoop Mathew and Bensiker Raja Singh D, ―Image Compression using Lifting based DWT‖, International Journal of computers, Information Technology and Engineering, Jan-June 2009.
- Elharar, Adrian Stern, OferHadar,“A Hybrid Compression Method for Integral Images Using Discrete Wavelet Transform and Discrete Cosine Transform”, Member, IEEE, and Bahram Javidi, Fellow, IEEE.
- B, Thiyagarajans. S, ―Hybrid Transformation technique for image compression‖,Journal of theoretical and applied information technology, 31st July 2012 Vol. 41 No.2.
- Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, Image quality assessment: From error visibility to structural similarity, IEEE Trans. on Image Processing, vol. 13, no. 4, pp. 600-612, Apr. 2004.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.





