How to Cite | Publication History | PlumX Article Matrix
De-noising Electroence phalogram (EEG) Signal using iterative Clipping Algorithm
Padmesh Tripathi and Abul Hasan Siddiqi
Department of Mathematics, School of Engineering and Technology, Sharda University 32-34, Knowledge Park- III, Greater Noida, India-201306.
Corresponding Author E-mail: padmesh01@rediffmail.com
DOI : http://dx.doi.org/10.13005/bbra/2470
ABSTRACT: Signal de-noising has been a topic of great interest for a long period. EEG is used to detect the neurological diseases. In the process of EEG recording, signal is contaminated due to several factors. Hence, for analysis of EEG signal in order to detect the diseases, it is necessary that signal must be de-noised first. Here, de-noising of signal is expressed as an inverse problem with total variation. This is an optimization problem. The solution of this optimization problem is obtained by using the iterative clipping algorithm. In this article, iterative clipping algorithm is used for de-noising EEG signal. To measure the performance of method, signal to noise ratio(SNR) and root mean square error(RMSE) have been calculated. It has been observed that the approach used here, works well in de-noising the EEG signal.
KEYWORDS: EEG; inverse problems; de-noising; total variation; iterative clipping algorithm
Download this article as:| Copy the following to cite this article: Tripathi P, Siddiqi A. H. De-noising Electroence phalogram (EEG) Signal using iterative Clipping Algorithm. Biosci Biotech Res Asia 2017;14(1). |
| Copy the following to cite this URL: Tripathi P, Siddiqi A. H. De-noising Electroence phalogram (EEG) Signal using iterative Clipping Algorithm. Biosci Biotech Res Asia 2017;14(1). Available from: https://www.biotech-asia.org/?p=21910 |
Introduction
Brain is one of the most important organs of human body which controls the coordination of muscles and nerves. Electroencephalogram (EEG) signal is a non-stationary biological signal and provides a lot of important information about different activities of the brain. It is the recording of electrical activity along the scalp with several electrodes placed on it over a short period of time. EEG is used to detect several neurological disorders.1,2 There are many factors which affect the recording and contaminate the EEG. Electrooculographic (EOG) is the most common physiological noise source that generates the EEG artefacts.3 Therefore, denoising plays a vital role in analysis of the EEG signal.
The problem of de-noising a signal is simply the noise removal from that signal. During last few decades, many techniques have been used to denoise (remove artefacts) the EEG signals. Kalman filters,4 adaptive filters,5,6 blind source separation (BSS) method,7 independent component analysis (ICA) have been applied8,9,10,11 in artifact removing. Lagerlund et al.12 explored the applications of principal component analysis (PCA) in removing artefacts from EEG signals. Wavelet and its several variants have been widely used in artefact removing from EEG.13,14 Empirical Mode Decomposition15,16 and ensemble empirical mode decomposition (EEMD) have been used in 17 and18 to remove different artefacts present in EEG.
Another method proposed by Rudin et al.,19 total variation denoising is used in signal and image processing. Rodriguez & Wohlberg,20 Hu & Jacob21 and Bredies et al.22 have applied it in image processing. In total variation regularization, minimization of a cost function produces the de-noising filter. All the algorithms that solve the optimization problem of de-noising can be used to implement the total variation regularization. So many methods are used to solve this problem. Selesnick and Bayram23 have developed an algorithm based on24 which has been used in this article.
Inverse problems deal with determining an input that produces an observed output, or determining an input that produces a desired output, often in presence of noise. Mathematically, let X and Y be spaces having appropriate structures such as Banach space, Hilbert space. Let A : X →Y be an operator which describes the relationship between the data y and the model parameter x. Direct problem: given the input x, find the output y; inverse problem: given an observed output y, find an input x that produces it. The solution minimizing
![]()
is known as total variation regularized solution. Here L is a smoothing and λ is regularization parameter. Regularization parameter λ plays important role in solving an inverse problem.25,26
In this article, iterative clipping algorithms proposed in23 have been used for de-noising EEG signal. Two performance measuring parameters, Signal to Noise Ratios (SNR) and Root Mean Square Errors (RMSE) have been calculated for different values of the regularization parameter λ. It has been observed that iterative clipping algorithm works well for de-noising the EEG signal.
Material and Methodology
Material
Data used here is taken from research project of Kocaeli University, Turkey, taken by Dr. Huya K. Sevindir on applications of wavelets methods to EEG data collected at the Hospital of Kocaeli University.27
Total Variation (TV) de-noising
The total variation of an N – point signal x (n),0 ≤ n ≤ N-1 is defined as
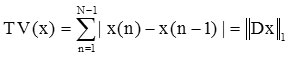
where D is an N-1 x N matrix.
Let be the measured (noisy) data of the form
![]()
where x(n) is (approximately) piecewise constant signal and ε(n) is white Gaussian noise. Then the inverse problem is to estimate x(n) given the noisy data y(n). TV de-noising estimates the signal x(n) by solving the optimization problem
![]()
The regularization parameter λ controls the degree of smoothing.18
Algorithm for TV de-noising
Problem (2) is solved by replacing D by A and formulating the dual by using an auxiliary vector z.5
The iterative clipping algorithm for TV de-noising is given by:

where α ≥ max eig (AAt).
Numerical implementation and performance analysis
Total variation de-noising based on (3) is implemented by the MATLAB program described in.23 Here α = 4 is set for de-noising. In the MATLAB program, D is implemented with the diff command. Number of iterations is kept fixed at 100 in algorithm.
To evaluate the performance, Signal to Noise Ratio (SNR) and Root Mean Square Error (RMSE) have been calculated for different values of regularization parameter λ in table1.
Table 1: Calculation of SNR and RMSE
| Values of λ | SNR | RMSE |
| 0.5 | 29.0011 | 0.1756 |
| 1.0 | 24.5130 | 0.2918 |
| 1.5 | 22.0242 | 0.3853 |
| 2.0 | 20.2630 | 0.4680 |
Figure 1 shows the original data while Figure 2, Figure 3, Figure 4 and Figure 5 show the de-noised data.
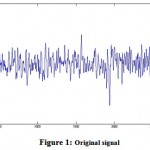 |
Figure 1: Original signal |
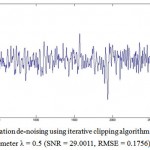 |
Figure 2: Total variation de-noising using iterative clipping algorithm for regularization parameter λ = 0.5 (SNR = 29.0011, RMSE = 0.1756)
|
 |
Figure 3: Total variation de-noising using iterative clipping algorithm for regularization parameter λ = 1(SNR = 24.5130, RMSE = 0.2918)
|
 |
Figure 4: Total variation de-noising using iterative clipping algorithm for regularization parameter λ = 1.5 (SNR = 22.0242, RMSE = 0.3853)
|
 |
Figure 5: Total variation de-noising using iterative clipping algorithm for regularization parameter λ = 2.0 (SNR = 20.2630, RMSE = 0.4680)
|
Results and Discussion
In this article, de-noising of EEG signal is modeled as an inverse problem with total variation and is expressed as the minimization of a non-differentiable cost function. Minimization of a non-differentiable cost function is a complex problem. It is minimized using the iterative clipping algorithm. It has been used for de-noising the EEG signal. More SNR implies more de-noising and on the contrary, more RMSE implies lesser de-noising. Table1 shows the values of SNR and RMSE for different values of λ. From the result obtained, we observe that iterative clipping algorithm works well for de-noising the EEG signal. We also observe that as λ increases, SNR decreases and RMSE increases. Figure1 represents the original data. Figure2 represents the de-noised data with SNR = 29.0011& RMSE = 0.1756for λ = 0.5, Figure3 represents the de-noised data with SNR = 24.5130& RMSE = 0.2918 for λ = 1.0, Figure4 represents the de-noised data with SNR = 22.0242 & RMSE = 0.3853 for λ = 1.5 and Figure5 represents the de-noised data with SNR = 20.2630 & RMSE = 0.4680 for λ = 2.0. Thus, through de-noising, the quality of EEG signal is enhanced.
Conclusions
Increased values of signal to noise ratio for different values of regularization parameter show that iterative clipping algorithm is suitable for de-noising the EEG signal. As the values of regularization parameter increase, the signal to noise ratio decreases and root mean square error increases. This shows that de-noising depends on the values of the regularization parameter. This is reflected from table1. The calculated SNR and RMSE for different values of regularization parameter show a satisfactory result.
References
- Binder D. K., Haut S. R. Towards new paradigms of seizure detection. Epilepsy Behaviours. 2013;26(3):247-523.
CrossRef - Boutros N. N., Struve F. Electrophysiological assessment of neuro psychiatric disorders. Seminars in Clinical Neuropsychiatry. 2002;7(1):30-41.
CrossRef - Croft R. J., Barry R. J. Removal of ocular artefact from the EEG: A review. Clinical Neurophysiology. 2000;30(1):5-19.
CrossRef - Sameni R., Shamsollahi M., Jutten C., Clifford G. A nonlinear Bayesian filtering framework for ECG denoising. IEEE Transactions on Biomedical Engineering. 2007;54(12):2172–2185.
CrossRef - He P., Wilson G., Russel C. Removal of ocular artefacts from electroencephalogram by adaptive filtering. Medical and Biological Engineering and Computing. 2004;42(3):407-412.
CrossRef - Sweeney K. T., Ayaz H., Ward T. E., Izzetoglu M., McLoone S. F., Onaral B. A methodology for validating artefact removal techniques for physiological signals. IEEE Transactions on Information Technology in Biomedicine. 2012;16(5):918-926.
CrossRef - Jung T. P., Makeig S., Humphries C., Lee T. W., McKeown M. J., Iragui V. Removing electroencephalographic artefacts by blind source separation. Psychophysilogy. 2000;37(2):163–178.
CrossRef - Ille N., Beucker R., Scherg M. Spatially Constrained independent component analysis for artefact correction in EEG and MEG. NeuroImage. 2001;13(6):159-159.
CrossRef - Flexer A., Bauer H., Priplf J., Dorffner G. Using ICA for removal of ocular artefacts in EEG recorded from blind subjects. Neural Networks. 2005;18(7):998-1005.
CrossRef - Krishnaveni V., Jayaraman S., Kumar P. M. M., Shivakumar K., Ramadoss K. Comparison of independent component analysis algorithms for removal of ocular artefacts from electroencephalogram. Measurement Science Review. 2005;5(2):67-78.
- Winkler I., Haufe S., Tangermann M. Automatic classification of artefactual ICA components for artefact removal in EEG signals. Behavioural and Brain Functions. 2011;7(30):1-15.
- Lagerlund T. D., Sharbrough F. W., Busacker N. E. Spatial filtering of multichannel electroencephalographic recordings through principal component analysis by singular value decomposition. Journal of Clinical Neurophysiology. 1997;14(1):73–82.
CrossRef - Krishnaveni V., Jayaraman S., Aravind S., Hariharasudhan V., Ramadoss K. Automatic identification and removal of ocular artefacts from EEG using Wavelet transform. Measurement Science Review Journal– Measurement in Biomedicine. 2006;6(4):45-57.
- Akhtar M. A., Mitsuhashi W., James C. Employing spatially constrained ICA and wavelet denoising for automatic removal of artefacts from multichannel EEG data. Journal of Signal Processing. 2012;92(2):401–416.
CrossRef - Raghavendra B. S., Dutt D. N. Correction of ocular artefacts in EEG recordings using empirical mode decomposition. Psychophysiology. 2010;47(5):955-960.
- Lindsen J., Bhattachatya J. Correction of blink artefacts using independent component analysis and empirical mode decomposition. Psychophysiology. 2010;47(5):955–960.
- Sweeney K., Ward T., McLoone S. Artefact removal in physiological signals—Practices and possibilities. IEEE Transanctions on Information Technology in Biomedicine. 2012;16(3):488–500.
CrossRef - Mijovi´c. B., DeVos M., Gligorijevic I., Taelman J., Huffel S. V. Source separation from single-channel recordings by combining empirical-mode decomposition and independent component analysis. IEEE Transactions on Biomedical Engineering. 2010;57(9):2188–2196.
CrossRef - Rudin L., Osher S., Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992;60:259-268.
CrossRef - Rodriguez P., Wohlberg B. Efficient minimization method for a generalized total variation functional. IEEE Transactions on Image Processing. 2009;18(2):322-332.
CrossRef - Hu Y., Jacob M. Higher degree total variation (hdtv) regularization for image recovery. IEEE Transactions on Image Processing. 2012;21(5):2559-2571.
CrossRef - Bredies K., Kunisch K., Pock T. Total generalized variation. SIAM Journal on Imaging Science. 2010;3(3):492-526.
CrossRef - Selesnick I., Bayram I. http://cnx.org/contents/8NLpidGL@1/total-Variation- Filtering, Accessed November 25. 2016.
- Chambolle A. Total variation minimization and a class of binary MRF models, In Energy Minimization Methods in Computer Vision and Pattern Recognition, Lecture Notes in Computer Sciences. Springer. 2000;3757:136-152.
CrossRef - Solo V. Selection of regularisation parameters for total variation de-noising, in Proc. IEEE international conference on Acoustics Speech Signal Processing. ICASSP. 1999;1653-1655.
- Wen Y. W., Chan R. H. Parameter selection for total-variation-based image restoration using discrepancy principle. IEEE Transactions on Image Processing. 2012;21(4):1770-1781.
CrossRef - Siddiqi A. H., Sevindir H. K., Aslan Z., Yazici C. Relevance of wavelets and inverse problems to brain. Proceedings of Satellite Conference. ICM ‘Mathematics in Science and Technology’ (Ed. Siddiqi et al.), World Scientific. 2010;402-429.

This work is licensed under a Creative Commons Attribution 4.0 International License.





