How to Cite | Publication History | PlumX Article Matrix
Study of Mechanical Energy Dissipation by Normal and Decalcified Animals Bones
Abdul Rauf1 and Syed Ismail Ahmad*2
1Department of Physics, College of Science, Jazan University, Jazan, Kingdom of Saudi Arabia.
2Department of General Science, Physics Division, Ibn Sina National College for Medical Studies, Jeddah- 21418, Kingdom of Saudi Arabia.
Corresponding Author E-mail: dr.syedismailahmad@gmail.com
DOI : http://dx.doi.org/10.13005/bbra/2728
ABSTRACT: The energy dissipated properties of normal and decalcified femur, rib and scapula bones of animals ox and camel have been studied by uniform bending technique. A hysteresis curve has been observed between the elevation in bone and load applied. It is observed that the energy dissipated as calculated from the hysteresis loop for rib is more than that of femur and scapula of ox and camel. It has been observed that the dissipation of energy in normal bone is less than that of decalcified bone under the same condition of applied load. The highest energy dissipation was observed in case of rib bone of camel compared to that of any other bone, rib of camel and scapula of ox dissipates maximum energy than femur bones. The study suggests that this technique is simple, elegant and inexpensive besides accurate in determining viscoelastic properties of bone.
KEYWORDS: Decalcification; Femur; Mechanical Energy Dissipation; Rib; Scapula; Uniform Bending
Download this article as:| Copy the following to cite this article: Rauf A, Ahmad S. I. Study of Mechanical Energy Dissipation by Normal and Decalcified Animals Bones. Biosci Biotech Res Asia 2019;16(1). |
| Copy the following to cite this URL: Rauf A, Ahmad S. I. Study of Mechanical Energy Dissipation by Normal and Decalcified Animals Bones. Biosci Biotech Res Asia 2019;16(1). Available from: https://bit.ly/2IcqxbW |
Introduction
Bone consists of lesser dense but hard and rigid tissue with some inorganic crystals which makes them stiff considerably. The organic part of the bone’s soft tissue is Collagen which has a Young’s modulus nearly equal to 1 GNm-2, whereas the Young’s modulus of bone itself is 11- 21 GNm-2. The Collagen gives strength to the bone despite of its softness. The bone can be considered as consist of hierarchically structured tiny crystals which makes them makes it very stronger.1,2 The bone is a biologically complex material which is being dominated by interfaces. The feature of bones inorganic frame work of calcareous material is that it lend itself more than any other tissue for mechanical strength and mechanical adaptations of the body. Extensive research and investigations has revealed that, in its internal structure, a bone is adapted in a extraordinary way to resist the stresses to which it is subjected during life of animals and human being. Extensive investigations have been made various research groups in recent past on mechanical properties of biological tissues, macromolecules, cells and organs in order to understand the mechanical behavior of different living systems. Research groups have measured the breaking point and the degree of stretching in human and animal tissues like human hair, skin and corium, tendons, cartilage of animals, frog muscle, the obtained values were compared with those of vulcanized rubber.3,4 Sodhi5 determined the biological prepattern of animals which is considered as the distribution of an inducing substance with regions of high and low concentration; which occur at sites. The process of distribution that arises is described.5 Some research groups have also determined the mechanical property, elasticity of cartilage, various long bones of human and ox, by using a modified Mangold elastometer and Gildemeister ballistic elastometer.
The mechanical property, Young’s modulus is an important property of bone, the augmentation in it with increasing (carbonated hydroxyapatite) cAp content emphasis cAp’s role in strengthening the collagen matrix.6 Some research groups have speculated that the cAp reinforces the composite by hindering sliding of collagen within the fibrils and the cAp actually does not carry load. The collagen distortion is an important component of load transfer. Burton7,8 determined the young’s modulus and elasticity of fibers and found that a sole fiber would appear stiffer than the aggregate or pile of fiber. Furthermore, he also reported the values of elastic modulus of smooth muscle of arterial wall. Survey of the literature reveals that the information about mechanical properties of soft tissue and muscle are present in large content but little work has been done and very less information is available on the important property, mechanical hysteresis of bone.
Therefore, in view of the scenario the present work is aimed to investigate and determine the mechanical hysteresis femur, rib and scapula bone of two different with different habitations the ox which lives in green habitation and camel which lives in desert, under normal and decalcinated conditions.
Material and Methods
Sample Preparation
Fresh samples of bovine bone were obtained from slaughter house and were boiled for two hours after removing flesh material and then kept exposed to air for seven days. Then they were cut into rectangular shaped bars of suitable dimensions along the bone axis. In order to determine the mechanical hysteresis, bone samples were made into bars by using bench type electrical grinder. The specimens then were decalcified by treating with 0.9% nitric acid for 24 hours and then suspended in running tap water for 24 hours. The mass of specimens was determined before and after the decalcification process.
Experimental
Uniform Bending Method
The elastic constant will be influenced by only such variables which can affect the atomic structure. The modulus of elasticity, which is a numerical measure of elasticity, has no relationship with elastic or proportional limit. In fact it is a measure of elastic stiffness of the material which in turn is equal to the slope of stress versus strain, (s – E) curve in the straight line region as shown in Fig. 1.
 |
Figure 1: A plot between stress (E) and strain (s).
|
Fig.2 shows the experimental arrangement to determine the Young’s modulus of bone by uniform bending method. K1 and K2 are the two knife edges on which the rectangular bar of specimen is placed. With the help of hangers equal loads M gm were suspended at the free ends at a distance of ‘a’ cm from its corresponding knife edge. Due to applied loads the bar bends uniformly. The elevation at the midpoint of the bar is measured with the help of dial gauge fixed over the bar.
A horizontal bar was kept on two knife edges and hangers were suspended at the edges of the bar. The dial gauge was fixed on the centre of the bar using retard stand as shown in Fig. 2. The distance between the two knife edges was measured using a Vernier calipers. Identical loads were suspended on both the ends at intervals of 50 gm. As a result the bar bends and dial gauge shows the reading for the elevation due to suspended load. To study the mechanical hysteresis of bone the elevation at the centre of the bone was measured for gradually increasing and decreasing of load at the interval of 50 gm.9
 |
Figure 2: Method of uniform bending –Experimental setup.
|
The area under the hysteresis loop, which is the energy stored was calculated using formula,
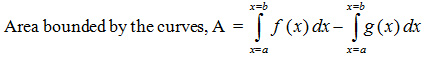
where f(x) & g(x) are the functions for the elevation with respect to the load for upper and lower curves respectively. The experiment was repeated for normal and decalcified bone. Data was tabulated for femur, rib and scapula of animals – ox and camel.
Results and Discussion
Table 1 shows the data pertaining to the energy dissipated calculated from the hysteresis for normal and decalcified bone specimens of femur, rib and scapula of Ox and Camel. A significant variation in this parameter is observed with respect to the type of bone (femur, rib and scapula); physiological condition (normal and decalcified) and the animal (ox and camel). Fig 3 shows the plots between elevation of bone on y-axis and applied load (increasing and decreasing) on x-axis for the bone specimens of femur, rib and scapula belonging to animals Ox and Camel, in their physiological conditions of normal and decalcified. It is interesting to observe mechanical hysteresis loops from the plots. The plots are used for the calculation of mechanical energy stored in the bone specimen.
The hard and soft tissues of vertebrate body provides a strong support to sustain against the gravitational force to the human and animal body. Most of the tissues in the vertebrate are soft tissues in nature, they are flexible and highly elastic. In the broad sense, their behavior is viscoelastic in nature.9,10 In contrast to the soft tissues the hard tissues are less elastic, more compact and rigid and they serve as endoskeleton and exoskeleton of the vertebrate body. Bone is a hard tissue made-up of both organic (collagen) and inorganic (calcium phosphate) materials. Hence it can be considered as viscoelastic biologically composite material. The organization of these hard and soft composite varies from animal to animal and is strongly influenced by physiological and anatomical alterations, in contrast to engineering composite materials.9 In general, determination of mechanical properties of entire or fraction of bone; or bone tissue is done by the same methods which are used to study the similar properties in metal and other structural composites and materials. These methods are based on the basic and fundamental principles of mechanics. In view of the above facts two animals have been selected for the study of mechanical adaptation of bone of an animal. One is camel which lives in desert and other one is Ox which lives in agricultural land.11-12
Table 1- Data on Energy dissipated by animal bone.
Table 1.1: Animal: Ox Bone: Femur.
| Sample Code | Energy Dissipated (´ 105 erg) | |
| Normal | Decalcified | |
| OF07 | 10.71 | 29.81 |
| OF08 | 09.09 | 62.50 |
| OF09 | 12.42 | 58.41 |
| OF10 | 10.02 | 92.88 |
| OF11 | 16.27 | 79.14 |
| OF12 | 07.70 | 29.08 |
Table 1.2: Animal: Ox Bone: Rib.
| Sample Code | Energy Dissipated (´105 erg) | |
| Normal | Decalcified | |
| OR07 | 28.59 | 51.24 |
| OR08 | 24.85 | 42.59 |
| OR09 | 23.62 | 53.89 |
| OR10 | 20.71 | 63.04 |
| OR11 | 25.82 | 95.29 |
| OR12 | 45.67 | 75.21 |
Table 1.3: Animal: Ox Bone: Scapula.
| Sample Code | Energy Dissipated (´105 erg) | |
| Normal | Decalcified | |
| OS07 | 30.00 | 072.38 |
| OS08 | 32.55 | 115.49 |
| OS09 | 46.76 | 116.76 |
| OS10 | 21.90 | 026.59 |
| OS11 | 23.13 | 029.97 |
| OS12 | 12.25 | 034.63 |
Table 1.4: Animal: Camel Bone: Femur.
| Sample Code | Energy Dissipated (´105 erg) | |
| Normal | Decalcified | |
| CF07 | 17.15 | 38.00 |
| CF08 | 09.09 | 28.66 |
| CF09 | 03.18 | 43.04 |
| CF10 | 17.88 | 34.16 |
| CF11 | 18.20 | 36.47 |
| CF12 | 20.40 | 52.57 |
Table 1.5: Animal: Camel Bone: Rib.
| Sample Code | Energy Dissipated (´ 105 ergs) | |
| Normal | Decalcified | |
| CR07 | 29.43 | 134.10 |
| CR08 | 21.62 | 118.37 |
| CR09 | 36.29 | 81.69 |
| CR10 | 45.32 | 68.80 |
| CR11 | 29.43 | 69.16 |
| CR12 | 31.79 | 41.23 |
Table 1.6: Animal: Camel Bone: Scapula.
| Sample Code | Energy Dissipated (´105 ergs) | |
| Normal | Decalcified | |
| CS07 | 12.53 | 26.35 |
| CS08 | 9.17 | 22.18 |
| CS09 | 11.54 | 10.39 |
| CS10 | 9.17 | 10.39 |
| CS11 | 13.68 | 25.82 |
| CS12 | 14.31 | 11.75 |
The capacity of bone to resist The mechanical forces and fractures withstanding capacity of bone mainly depends on the quality and quantity of bone which will be characterized by the microstructure, shape and geometry of bones, collagen and mineral that dominate at the nanoscale and the rate of bone turnover. There will be a complex structure that influences the mechanical and fracture properties of bone.13 Two conditions, normal and decalcified, have been considered in order to assess the influence of calcium phosphate on mechanical hysteresis of bone. Different bones in the same animal have different mechanical properties due to their adaptations. Hence, the results on mechanical hysteresis reveal considerable variation in these mechanical properties.14,15 The data reveals that the elevation during loading the specimen is different from the elevation during unloading the specimen. There is a certain lag in the path traced during two cases. This shows that during unloading energy is being dissipated by the material. When the data relating elevation to load was traced, two curves were obtained, one for loading and other for unloading the same specimen, showing a hysteresis. Some of the representative plots are shown in Fig.3.
Table 2: A Comparison on average values of Energy Dissipated by Normal and Decalcified Animal bone.
| Animal | Bone | Energy dissipated | |
| ( x 105 erg) | |||
| Normal | Decalcified | ||
| OX | Femur | 11.03 | 58.63 |
| ± 2.74 | ± 23.49 | ||
| Rib | 28.21 | 63.54 | |
| ± 8.15 | ± 17.45 | ||
| Scapula | 27.76 | 65.97 | |
| ± 10.68 | ± 38.51 | ||
| Camel | Femur | 14.31 | 38.81 |
| ± 6.11 | ± 7.5 | ||
| Rib | 32.31 | 85.55 | |
| ± 7.25 | ± 31.52 | ||
| Scapula | 12.24 | 17.81 | |
| ± 1.8 | ± 7.10 | ||
 |
Figure 3: Hysteresis loop due to elevation in animal bone versus load applied by using uniform bending method.
|
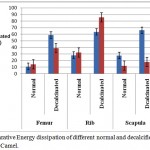 |
Figure 4: Comparative Energy dissipation of different normal and decalcified bones of Ox and Camel.
|
The area under the hysteresis curves was proved to be the amount of energy dissipated. The amount of energy was calculated using integral calculus method and tabulated in Table 2. The energy dissipated is more for rib when compared with femur and scapula for both the animals – ox and camel. It has been observed that the dissipation of energy in normal bone is less than that of decalcified bone under the same condition of applied load, as shown in Fig.4. The energy dissipation of rib bone of camel is more than that of any other bone, rib of camel and scapula of ox maximum energy dissipation than that of femur bone for ox and scapula of camel.9,15,16
Conclusion
Mechanical energy dissipation of femur, rib and scapula bones of two animals ox and camel with different adaptations under normal and decalcified conditions has been successfully investigated using uniform bending techniques. The elevation at the centre of bones during loading and unloading was different in all the bones in both physiological conditions showing a hysteresis, bone can be considered as a composite viscoelastic material. The property Viscoelastisity of the bone varies from animal to animal, type bone and strongly depends on anatomical conditions unlike engineering composite materials, energy in decalcinated bones found to be more than that of normal bones. The rib bone of desert animal camel shows the highest viscoelasticity compared to other bones.
References
- Stock S. R. The Mineral–Collagen Interface in Bone.Calcified Tissue Intl. 2015;97(3):262–280. doi: 10.1007/s00223-015-9984-6.
- Weiner S., Wagner H. D. The material bone: structure-mechanical function relations. Annu Rev Mater Sci. 1998;28:271–298.
- Posner A. S. The structure of bone apatite surfaces. J Biomed Mater Res. 1985;19:241–250. [PubMed: 3001090]
- Meyers A.´M., Po-Yu C., Yu-Min L. A., Seki Y. Biological materials: Structure and mechanical properties. Progress. Mater. Sci. 2008;53:1–206
- Sondhi K. C. The Biological Foundations of Animal Patterns. The Quarterly Rev. Bio. 1963;38(4):289-327.
- John D. Currey. (ed): Bones: Structure and Mechanics. 2nd Edition. Princeton Univ Press; Princeton. 2006;55-134.
- Lucchinetti E. Composite models of bone properties. In: Bone mechanics handbook. 2. (Cowin, SC, ed). New York: CRC Press. Boca Raton. 2001;12-1-12-19.
- Burton A. C. Relation of structure to function of the tissues of the wall of blood vessels. Physiol Rev. 1954;34(4):619-642.
- Rauf A.,Sattar A. Study on Thermal and Mechanical properties of animal Bone. PhD Thesis. JNTUH Hyderabad. March. 2009 .
- Liu X., Dean N. M., Youssefpour H.,Summers P. A., Earthman C. J. Stress relaxation behavior of tessellated cartilage from the jaws of blue sharks. J. Mech. Behavior Biomed Mater. 2014;29:68–80. http://dx.doi.org/10.1016/j.jmbbm. 2013.08.014.
- Bankoff P. D. A. Biomechanical Characteristics of the Bone, Human Musculoskeletal Biomechanics, Dr. Tarun Goswami (Ed.). ISBN: 978-953-307-638-6. In Tech. 2012.
- Pioletti P. D., Rakotomanana R. L. Non-linear viscoelastic laws for soft biological tissues. Eur. J. Mech. A/Solids. 2000;19:749–759.
- Launey M. E., Buehler M. J., Ritchie R. O. On the Mechanistic Origins of Toughness in Bone. Annual Rev Mater Rese. 2010;40:25-53.
- Blaisdell F. A (ed): A Practical Physiology: A Text-Book for Higher Schools. Project Gutenberg Licensed eBook- online at www.gutenberg.net. 2003 [EBook #10453]
- Sierpowska J (ed). Electrical and Dielectric Characterization of Trabecular Bone Quality. PhD Thesis, Faculty of Natural and Environmental Sciences. University of Kuopio. 2007.
- Rauf A. A review on mechanical properties of animal bone. International Journal of Science, Environment and Technology. 2014;3(4):1419–1435.

This work is licensed under a Creative Commons Attribution 4.0 International License.





