Manuscript accepted on : July 02, 2009
Published online on: 28-06-2010
Swapnaja Ashish Mohite* and Ashish Suresh Mohite
College of Fisheries, Ratnagiri, Maharashtra India. Corresponding Author E-mail: sa_mohite@yahoo.co.in
ABSTRACT: The shell dimensions (length, height, width) and total weight as well as wet weight of Paphia malabarica as estimators of growth were evaluated in the clams cultured in two intertidal areas of Ratnagiri, India during the present study. The b values for all relationships were significantly different from zero. The results show a strong linearity between the total weight and wet weight to the shell length. The b values for the length-weight relationship were within the range for other bivalves. The dimensional relationship showed difference in the clam stocks present at Kalbadevi and Kajali estuaries at Ratnagiri (west coast), India.
KEYWORDS: Paphia malabarica; length - weight relationship; total weight; wet weight
Download this article as:| Copy the following to cite this article: Mohite S.A,Mohite A.S . Allometric Relationships in the Shortneck Clam Paphia Malabarica (Chemnitz) Cultured in the Estuarine Areas of Ratnagiri, India.Biosci Biotechnol Res Asia 2010;7(1) |
| Copy the following to cite this URL: Mohite S.A,Mohite A.S . Allometric Relationships in the Shortneck Clam Paphia Malabarica (Chemnitz) Cultured in the Estuarine Areas of Ratnagiri, India.Biosci Biotechnol Res Asia 2010;7(1). Available from: https://www.biotech-asia.org/?p=9070 |
Introduction
Paphia malabarica is an important venerid clam, found in the Kalbadevi estuary (Shirgaon creek) and Kajali estuary (Bhatye creek), Ratnagiri. They are exploited on commercial basis throughout the year. Attempts were made to culture these clams in these estuarine areas. Studying the growth in theses clams and establishing allometric relationships are essential for generating information for managing the resources and understanding the effects of the changing environmental conditions on the growth pattern. This would also help in managing the fast depleting resources of clams from the estuarine areas along the coast of Ratnagiri, India.
Often growth is estimated by measuring shell dimensions and the weight of wet tissue or the volume of the animal (Hibbert 1977, Bailey and Green 1988). From the established allometric relationships, estimations of the biomass and total meat production can be made. This study was conducted to determine whether shell dimensions (length, height, width) and total weight as well as weight of the wet tissue have strong relationship that can be used to monitor biomass production in populations of P. malabarica in estuarine areas of Ratnagiri (west coast of India). The study also done to establish the dimensional relationship between the clam stocks of two estuarine regions viz. Kalbadevi estuary (Shirgaon) and Kajali estuary (Bhatye).
Materials and methods
The data was collected from February 2004 to January 2006 from the clams cultured in the intertidal areas of Kalbadevi (Shirgaon station) and Kajali (Bhatye station) estuaries of Ratnagiri. The clams for stocking were collected from the respective estuary in the shell length range of 22-30 mm. From these, 3256 specimens were collected from Shirgaon and 3338 specimens were collected from Bhatye, at fortnightly intervals. Both the stations were sampled on the same day by using quadrants with the area of 1 m3. Shell length of each specimen was measured upto 0.1 mm using vernier calipers. Total weight measurements were made to the nearest 0.01 g after drying the shell with paper towels. The wet tissues were blotted and their weight was measured to the nearest 0.001 g with a Sartorius electronic balance. The data on the shell lengths for two fortnights in each month were pooled together (Joseph and Joseph, 1985). All morphological measurements such as shell length, height, width, total weight, wet weight and dry weight were measured following the method adopted by Abraham (1953). Regressions of height, width, total weight, wet weight and dry weight on shell length were studied by the simple equation for linear regression Y = a Xb, where Y is taken as height (Ht.), width (Wd.), total weight (Wt.), wet weight (WWt.) and dry weight (dWt.). X is taken as shell length (Lt.). ‘a’ and ‘b’ are constants to be determined empirically.
The data from the linear relationships was used to understand the variations, if any between clams representing the two different habitats i.e Shirgaon and Bhatye. The relationship was studied by using the allometric relationships calculated earlier. To testify the degree of association between different dimensions, of clam populations, from different habitats, following equations developed by Newcomb (1926) were used.
α = β = γ ………………Eqn A.
α = (b3 – b2 -1) / b1 ………………Eqn B.
β = (b3 – b1 -1) / b2 ………………Eqn. C.
γ = (b3 – b1 – b1) ………………Eqn. D.
Where b1 is the constant in length – height relationship, b2 is the constant in length – width relationship and b3 is the constant in length – weight relationship.
Results and discussion
Allometric relationships between whole body weight, length, width, height, wet weight and dry weight were studied from Shirgaon and Bhatye. The present study on the relationship between various parameters of P. malabarica would help future works on culture aspects of this clam.
The constants were determined from the morphological data collected bimonthly from both the stations. The relationships between length and total weight, length and width, length and height, length and wet weight and dry weight and wet weight were calculated for the clams collected from Shirgaon and Bhatye. The relationships were determined using the simple linear equations, where Ht is shell height, Wd is width, Wt is total weight, L is shell length, Wwt is wet weight, Dwt is dry weight. The regression analysis of the allometric data is presented in Table 1 for Shirgaon population and Table 2 for Bhatye. The data is represented by Fig. No. 1 to 14.
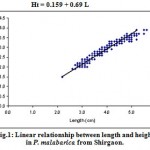 |
Figure 1: Linear relationship between length and height in P. malabarica from Shirgaon.
|
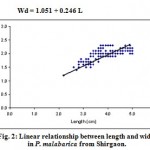 |
Figure 2: Linear relationship between length and width in P. malabarica from Shirgaon.
|
 |
Figure 3: Logarithmic relationship between length and total weight in P. malabarica from Shirgaon.
|
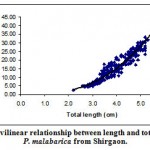 |
Figure 4: Curvilinear relationship between length and total weight in P. malabarica from Shirgaon.
|
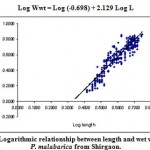 |
Figure 5: Logarithmic relationship between length and wet weight in P. malabarica from Shirgaon.
|
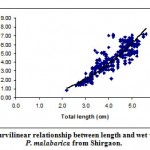 |
Figure 6: Curvilinear relationship between length and wet weight in P. malabarica from Shirgaon.
|
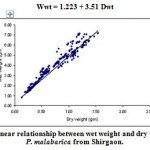 |
Figure 7: Linear relationship between wet weight and dry weight in P. malabarica from Shirgaon.
|
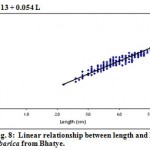 |
Figure 8: Linear relationship between length and height in P. malabarica from Bhatye.
|
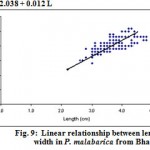 |
Figure 9: Linear relationship between length and width in P. malabarica from Bhatye.
|
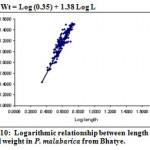 |
Figure 10: Logarithmic relationship between length and total weight in P. malabarica from Bhatye.
|
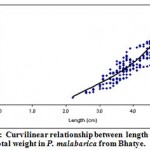 |
Figure 11: Curvilinear relationship between length and total weight in P. malabarica from Bhatye.
|
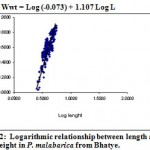 |
Figure 12: Logarithmic relationship between length and wet weight in P. malabarica from Bhatye.
|
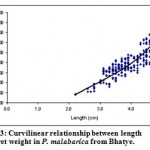 |
Figure 13: Curvilinear relationship between length and wet weight in P. malabarica from Bhatye.
|
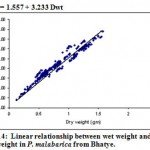 |
Figure 14: Linear relationship between wet weight and dry weight in P. malabarica from Bhatye.
|
Shafee (1976) has studied various relationship between whole body weight, length, breadth, height, shell weight, soft body weight and dry body weight in the intertidal green mussel, Perna viridis of Ennore estuary, Madras. The study was done based on the Principal Component Analysis and least square technique. Both these studies confirmed the observations that there was a difference in growth pattern between mature and immature mussels. Modassir (1990) has worked on M. casta from Mandovi estuary, Goa. An equation of Y = – 0.6228 + 3.233 X was estimated for M. casta, using the regression of total weight on shell length.
All the slopes of the regression lines are significantly different from zero. Height, width, total weight of the clam and wet weight show a strong correlation with the shell length. The results show a strong linearity between the total weight and wet weight to the shell length. The b values for the length-weight relationship are within the range for other bivalves (Park and Oh 2002).
malabarica inhabits the intertidal zones of the Kalbadevi and Kajali estuaries and is subjected to long period of submergence. These clams are potentially exposed to desiccation and a wide range of salinity as well as fluctuating pH and temperature. These clams have thicker shells, which make the clams heavier. The adverse intertidal conditions might direct the allocation of energy to shell growth instead of soft tissue, that might limit the growth on an individual (Curry 1988). The need for thicker shells than normal was also reported in Mytilus edulis inhabiting periodically dry zones (Seed 1968, Gimin et al. 2004) and is common in shell bearing molluscs living in intertidal or shallow, marine environments (Tokeshhi et al. 2000). The low rate of tissue growth helps in survival of the clams under prolonged exposure by maintaining a large volume of water inside the shell for
Table 1: Allometric relationships between morphometric characters of P. malabarica from Shirgaon.
| Parameters | Equation | ||||
| a | b | r | n | ||
| Height (Ht.) on length (L) | Ht = 0.159 + 0.69 L | 0.159 | 0.69 | 0.951* | 600 |
| Width (Wd.) on Length (L.) | Wd = 1.051 + 0.246 L | 1.051 | 0.246 | 0.638* | 600 |
| Total weight (Wt) on length (L) | Log Wt =Log ( -0.49) + 2.77 Log L
|
-0.49 | 2.77 | 0.948* | 600 |
| Wet weight (Wwt) on Length (L) | Log Wwt = Log (-0.698) + 2.129 Log L | – 0.698 | 2.129 | 0.906* | 600 |
| Wet weight (Wwt) on dry weight (Dwt) | Wwt = 1.223 + 3.51 Dwt | 1.223 | 3.51 | 0.882* | 600 |
r = correlation coefficient, n = number of specimens.
* Significant (P< 0.05)
Table 2: Allometric relationships between morphometric characters of P. malabarica from Bhatye.
| Parameters | Equation | ||||
| a | b | r | n | ||
| Height (Ht.) on length (L) | Ht = 2.713 + 0.054 L | 2.713 | 0.054 | 0.277* | 600 |
| Width (Wd.) on Length (L.) | Wd = 2.038 + 0.012 L
|
2.038 | 0.012 | 0.129* | 600 |
| Total weight (Wt) on length (L) | Log Wt = Log (0.35) + 1.38 Log L
|
0.35 | 1.38 | 0.692* | 600 |
| Wet weight (Wwt) on Length (L) | Log Wwt = Log (-0.073) + 1.107 Log L
|
– 0.073 | 1.107 | 0.675* | 600 |
| Wet weight (Wwt) on dry weight (Dwt) | Wwt = 1.557 + 3.233 Dwt | 1.557 | 3.233 | 0.874* | 600 |
r = correlation coefficient, n = number of specimens.
* Significant (P< 0.05)
survival of body tissue. The faster rate of tissue growth would allow a much smaller space for the intake of water that is necessary to support the metabolic needs of the increased tissue. The shell growth hence is not accompanied by the increase in tissue weigh.
Table 3: Calculated values of α, β and γ for P. malabarica from Shirgaon and Bhatye.
| Locality | α | β | γ | Average |
| Shirgaon | 1.2629 | 1.4652 | 1.254 | 1.327 |
| Bhatye | 0.2867 | – 0.745 | 0.607 | 0.149 |
Data on the dimensional relationships of P. malabarica studied earlier from Shirgaon and Bhatye were fitted into the above equations (Table 3). It was seen that the Equation A did not hold well in the case of both the stations, thus reflecting on the differences in the dimensional relationship amongst the two clam stocks. The clam populations at both the stations also showed the differences in the morphometric parameters. These differences could be directly correlated to the differences in the ecological conditions present at the two stations. Parulekar et al., (1973) have reported the existence of different clam stocks M. casta in the estuarine systems of Goa based on the similar dimensional studies.
From the present study, it can be concluded that shell dimensions can not be used as good estimators for the biomass of P. malabarica to understand the growth of the clams during the culture period. The allometric relationships between the shell length, width, height, total weight and wet weight can be used to monitor the growth of this species in the estuarine areas.
References
- Bailey, R. C. and Green, R. H., Within-basin variation in the shell morphology and growth rate of freshwater mussel. Can. Jour. Zool. 66: 1704-1708 (1988)
- Curry, J.D., Shell form and strength, In E.R. Trueman and M.R. Clarke (Eds.).The Mollusca: Form and function. Academic Press, London. pp.183-210 (1988).
- Gimin, R., R. Mohan, Thinh, L.V. and Griffiths, A.D., The relationship of shell dimensions and shell volume to live weight and soft tissue weight in the mangroveclam, Polymesoda erosa (Solander, 1786) from northern Australia. Naga, WorldFish Center Q. 27 (3 & 4), 32 – 35 (2004).
- Hibbert, C.J., Growth and survivorship in a tidal flat population of the bivalve Mercenaria mercenaria from Souththampton Waters. Mar. Biol. 44, 71-76 (1977).
- Joseph, M.M. and Joseph, P. S., Age and growth of the oyster Crassostrea madrasensis (Preston) in Mulki estuary, west coast of India. Indian Jour. Mar. Sci., 14, 184-186 (1985).
- Modassir, Y., Ecology and production of benthic bivalve Meretrix casta (Chemnitz) in Mandovi estuary, Goa. Indian Jour. Mar. Sci., 19, 125- 127 (1990).
- Park, K.Y. and Oh, C.W., Length- weight relationship of bivalves from coastal waters of Korea. Naga ICLARM Q. 25 (1), 21-22 (2002).
- Parulekar, A.H., Dwivedi, S.N. and Dhargalkar, V.K., Ecology of clam beds in Mandovi, Cumbarjua canal and Zuari estuarine system of Goa. Indian Jour. Mar. Sci., 2, 122-126 (1973).
- Seed, R., Factors influencing shell shape in the mussel Mytilus edulis. Jour. Mar. Biol. Ass. U.K. 48, 561-584 (1968).
- 10.Shafee, M.S., Studies on the various allometric relationships in the intertidal green mussel, Perna viridis Linneaus of Ennore estuary, Madras. Indian Jour. Fish. 23 (1and 2), 1 – 9 (1976).
- Tokeshhi, M., Ota, N. and Kawai, T., A comparative study of morphometry in shell- bearing molluscs. J.Zool. Lond. 251, 31 – 38 (2000).

This work is licensed under a Creative Commons Attribution 4.0 International License.





